Verteilungsfunktion (empirisch)

Grundbegriffe

Empirische Verteilungsfunktion

Die Ermittlung von empirischen Verteilungsfunktionen setzt skalierte Merkmalsausprägungen voraus, d.h. mindestens ordinal- oder kardinalskalierte Merkmale.

Empirische Verteilungsfunktion eines diskreten (nicht klassierten) Merkmals

Für die empirische Verteilungsfunktion eines diskreten (nicht klassierten) Merkmals gilt:

$F(x)={\begin{cases}0&{\mbox{, falls }}x<x_{1}\\\sum _{i=1}^{j}f\left(x_{i}\right)&{\mbox{, falls }}x_{j}\leq x<x_{j+1}\\1&{\mbox{, falls }}x_{k}\leq x\end{cases}}$

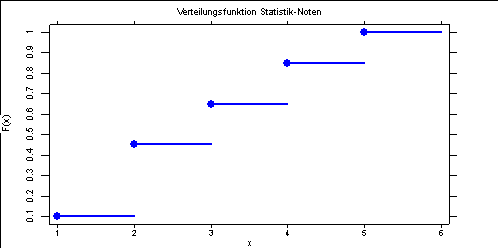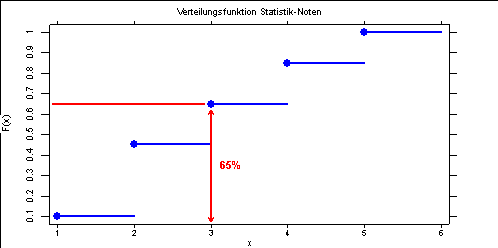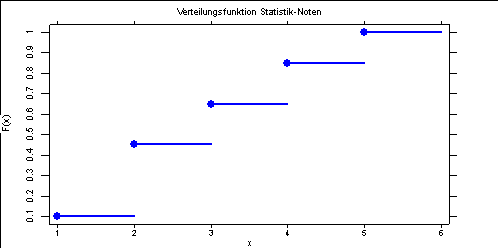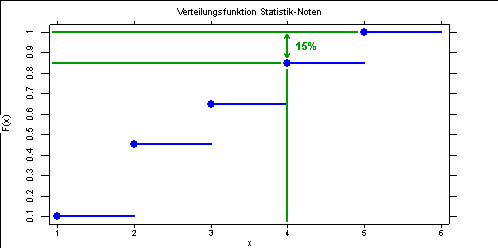
Die grafische Darstellung der empirischen Verteilungsfunktion ergibt bei diskreten (nicht klassierten) Merkmalen eine monoton wachsende Treppenfunktion. Sie "springt" um die zu jeder Merkmalsausprägung dazugehörige relative Häufigkeit.

Empirische Verteilungsfunktion eines kardinalskalierten klassierten Merkmals

Für die empirische Verteilungsfunktion eines kardinalskalierten klassierten Merkmals gilt:

$F(x)={\begin{cases}0&{\mbox{, falls }}x<x_{1}^{u}\\\sum _{i=1}^{j-1}f\left(x_{i}\right)+{\frac {x-x_{j}^{u}}{x_{j}^{o}-x_{j}^{u}}}\cdot f\left(x_{j}\right)&{\mbox{, falls }}x_{j}^{u}\leq x<x_{j}^{o}\\1&{\mbox{, falls }}x_{k}\leq x\end{cases}}$

Die empirische Verteilungsfunktion bei klassierten Merkmalen gibt an, wie viele Ausprägungen insgesamt unterhalb der jeweiligen oberen Klassengrenze liegen.

In der grafischen Darstellung der empirischen Verteilungsfunktion werden die sich ergebenden einzelnen Punkte geradlinig zu einer stückweise linearen Kurve (Polygonzug) verbunden.

Interpolation

Mittels einer Interpolation der empirischen Verteilungsfunktion $F(x)$ eines kardinalskalierten klassierten Merkmals kann der Wert der Verteilungsfunktion für jedes $x$ im beobachteten Bereich des Merkmals $X$ approximativ bestimmt werden.

$F\left(x\right)=F\left(x_{j}^{u}\right)+{\frac {x-x_{j}^{u}}{x_{j}^{o}-x_{j}^{u}}}\cdot f(x_{j})$

Grafische Veranschaulichung der Interpolation:

Beispiele

Statistik-Prüfung

In der Statistik-Prüfung haben 20 Studenten folgende Noten erzielt:

2, 2, 4, 1, 3, 2, 5, 4, 2, 4, 3, 2, 5, 1, 3, 2, 2, 3, 5, 4

Die Verteilung der Noten lässt sich übersichtlich in Form einer Häufigkeitstabelle darstellen:

Note $X$	absolute Häufigkeit $h\left(x_{j}\right)$	relative Häufigkeit $f\left(x_{j}\right)$	Empirische Verteilungsfunktion $F\left(x_{j}\right)$
1	2	0,10	0,10
2	7	0,35	0,45
3	4	0,20	0,65
4	4	0,20	0,85
5	3	0,15	1,00

Die Verteilungsfunktion lässt sich grafisch darstellen:

Die Tabelle bzw. die Grafik lässt beispielsweise folgende Interpretationsmöglichkeiten zu:

• 65% der 20 Studenten (= 13) haben die Note 3 oder besser erreicht.
• 15% (100% - 85%) der 20 Studenten (= 3) haben die Prüfung nicht bestanden.

Haushaltsgröße (empirische Verteilungsfunktion, diskret, nicht klassiert)

Empirische Verteilungsfunktion der Haushaltsgröße 1990:

Haushaltsgröße	$f\left(x_{j}\right)$	$F\left(x_{j}\right)$
1	0,350	0,350
2	0,302	0,652
3	0,167	0,819
4	0,128	0,947
5 und mehr	0,053	1,000

Mittels der empirischen Verteilungsfunktion lässt sich die relative Häufigkeit berechnen:

$f\left(x_{j}\right)=F\left(x_{j}\right)-F\left(x_{j-1}\right)$ für $j=1,\ldots ,k$ mit $F\left(x_{0}\right)=0$.

Es gilt:

$f(x_{j}<X<x_{h})=f(x_{j}<X\leq x_{h-1})=f(X\leq x_{h-1})-f(X\leq x_{j})=F(x_{h-1})-F(x_{j})$

Lebensdauer von Glühlampen (empirische Verteilungsfunktion, kardinalskaliert, klassiert)

Untersuchung der Lebensdauer (in Stunden) von 100 Glühlampen:

statistische Einheit:	Glühlampe
statistisches Merkmal:	Lebensdauer
	kardinalskaliert, stetig

$x_{j}^{u}\leq X<x_{j}^{o}$	$h\left(x_{j}\right)$	$f\left(x_{j}\right)$	$F\left(x_{j}\right)$
0-100	1	0,01	0,01
100-500	24	0,24	0,25
500-1000	45	0,45	0,70
1000-2000	30	0,30	1,00
Summe	100	1.00

Die empirische Verteilungsfunktion der Lebensdauer von Glühlampen hat die folgende Form:

Die geradlinige Verbindung der Punkte in der grafischen Darstellung erfolgt ausgehend von der Annahme einer gleichmäßigen Verteilung der Ausprägungen innerhalb einer Klasse.

Benzinverbrauch (empirische Verteilungsfunktion, kardinalskaliert, klassiert)

Von 74 verschiedenen Autotypen wurde der Benzinverbrauch in "miles per gallon" (mpg) gemessen - Umrechnung in l/100km: $(3,785\cdot 100)/(x\cdot 1,61).$

Das Ergebnis der Untersuchung lässt sich übersichtlich in Form einer Häufigkeitstabelle darstellen:

Benzinverbrauch(MPG) $x_{j}^{u}\leq X<x_{j}^{o}$	absolute Häufigkeit $h\left(x_{j}\right)$	relative Häufigkeit $f\left(x_{j}\right)$	Empirische Verteilungsfunktion $F(x_{j})$
12 bis < 15	8	0,108	0,108
15 bis < 18	10	0,135	0,243
18 bis < 21	20	0,270	0,513
21 bis < 24	13	0,176	0,689
24 bis < 27	12	0,162	0,851
27 bis < 30	4	0,054	0,905
30 bis < 33	3	0,041	0,946
33 bis < 36	3	0,041	0,987
36 bis < 39	0	0,000	0,987
39 bis < 41	1	0,013	1,000
Summe	74	1,000

Die empirische Verteilungsfunktion lässt sich in Form eines Histogramms mit der gleichen Klassenbreite wie in der Häufigkeitstabelle (3 Meilen) grafisch veranschaulichen. Auf der Ordinatenachse werden die Häufigkeitsdichten abgetragen.

Die geradlinige Verbindung der Punkte in der grafischen Darstellung erfolgt ausgehend von der Annahme einer gleichmäßigen Verteilung der Ausprägungen innerhalb einer Klasse.

Aus der empirischen Verteilungsfunktion lässt sich beispielsweise ablesen, dass 68,9 Prozent der untersuchten Autotypen weniger als 24 Meilen mit einer Gallone fahren können, das heißt, einen Benzinverbrauch von mehr als 9,8 Litern aufweisen.