Grafische Darstellung diskreter Merkmale
Aus MM*Stat
Unterseiten Beispiel: Stellung im Beruf (Kreisdiagramm und Säulendiagramm) • Beispiel: Haushaltsgröße (Säulendiagramm) |
Grafische Darstellung diskreter Merkmale
Für die grafische Darstellung der eindimensionalen Häufigkeitsverteilung diskreter Merkmale gibt es verschiedene Möglichkeiten: Säulen- bzw. Balkendiagramm, Kreisdiagramm, Rechteck- bzw. Flächendiagramm, Stab- bzw. Liniendiagramm, Piktogramm oder Kartogramm.
Säulen- oder Balkendiagramm
Das Säulen- oder Balkendiagramm dient der grafischen Darstellung der empirischen Häufigkeitsverteilung vor allem von nominalskalierten und ordinalskalierten Merkmalen, aber auch von metrisch skalierten diskreten Merkmalen mit wenigen Merkmalsausprägungen.
Ein Balkendiagramm stellt die Häufigkeit jeder Merkmalsausprägung als separaten Balken dar. Dazu werden auf der Abszissenachse die Merkmalsausprägungen und auf der Ordinatenachse die beobachtete absolute oder relative Häufigkeit der jeweiligen Merkmalsausprägung abgetragen.
Im Allgemeinen handelt es sich hierbei um eine höhenproportionale Darstellung.
In der folgenden Grafik werden die relativen Häufigkeiten in Prozent verwendet:
Kreisdiagramm
Ein Kreisdiagramm stellt die Häufigkeit jeder Merkmalsausprägung durch die Aufteilung einer Kreisfläche in Sektoren dar.
Im Allgemeinen handelt es sich um eine flächenproportionale Darstellung.
Rechteck- oder Flächendiagramm
Ein Rechteck- oder Flächendiagramm stellt die Häufigkeit jeder Merkmalsausprägung durch die Aufteilung einer Fläche in einzelne Bereiche dar.
Im Allgemeinen handelt es sich um eine flächenproportionale Darstellung.
In der folgenden Grafik werden die relativen Häufigkeiten in Prozent verwendet:
Stab- oder Liniendiagramm
Ein Stab- oder Liniendiagramm stellt die Häufigkeit jeder Merkmalsausprägung durch die Höhe von Säulen dar (vgl. Säulendiagramm).
Im Allgemeinen handelt es sich um eine höhenproportionale Darstellung.
Piktogramm
Ein Piktogramm stellt die Häufigkeit jeder Merkmalsausprägung mit unterschiedlich großen Bildsymbolen oder einer verschieden großen Anzahl von Bildsymbolen dar. Dabei muss die ausgewählte Größe des Bildsymbols bzw. die Anzahl der Bildsymbole die dafür stehende Häufigkeit abbilden.
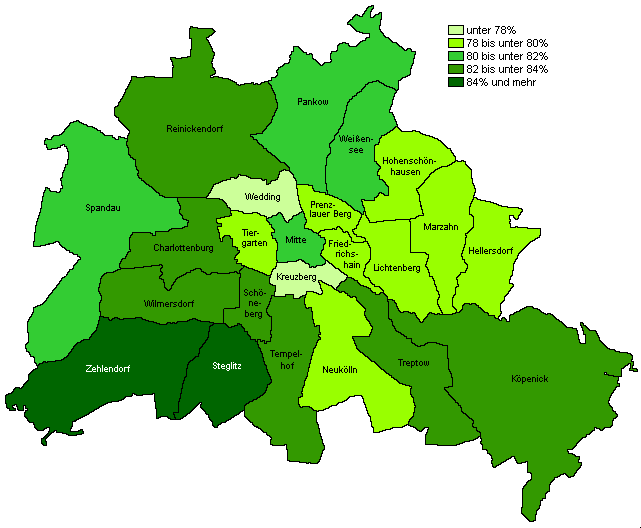
Kartogramm
Ein Kartogramm stellt die Häufigkeit jeder Merkmalsausprägung innerhalb einer Landkarte dar.