Unabhängige Ereignisse: Unterschied zwischen den Versionen
Aus MM*Stat
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Wahrscheinlichkeitsrechnung}} | {{Wahrscheinlichkeitsrechnung}} | ||
{{SubpageToc|Beispiel: Corona-Risiko}} | |||
=={{Vorlage:Überschrift}}== | =={{Vorlage:Überschrift}}== | ||
Aktuelle Version vom 7. August 2020, 07:27 Uhr
Unterseiten |
Grundbegriffe
Unabhängige Ereignisse
Wir haben gesehen, dass im allgemeinen die Vorinformation über das Eintreten von Ereignissen die Wahrscheinlichkeit für das Auftreten anderer Ereignisse beeinflusst. Im Allgemeinen gilt also:
Wenn aber ist, so hängt das Eintreten von nicht von dem Eintreten (oder Nichteintreten) des Ereignisses ab.
und sind dann voneinander unabhängige Ereignisse (stochastische Unabhängigkeit). Denn wenn unabhängig ist von , so ist auch unabhängig von .
Dann muss gelten:
Zusatzinformationen
Unabhängig disjunkt
Beachten Sie den Unterschied zwischen den Begriffen "unabhängig" und "disjunkt":
Sind zwei Ereignisse und mit und disjunkt, dann gilt:
wegen für die Wahrscheinlichkeit: ;
aber
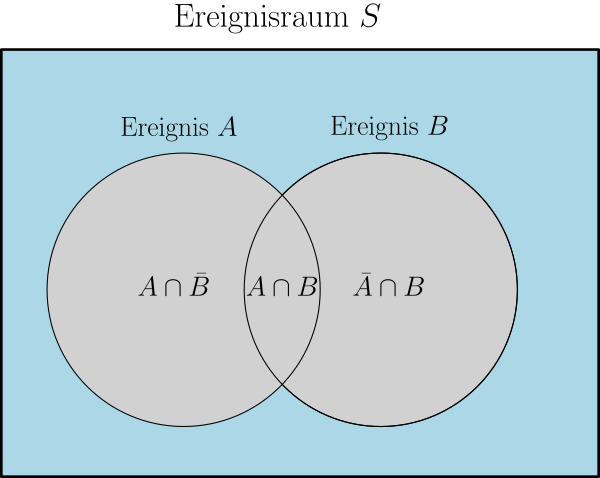
Also gilt, dass und nicht unabhängig voneinander sein können, sofern sie disjunkt sind, und dass falls sie unabhängig voneinander sind, sie eine gemeinsame Schnittmenge besitzen müssen.
Somit schließen sich disjunkt und unabhängig gegenseitig aus.
Herleitung von Beziehungen bei Unabhängigkeit
Zu zeigen ist: Bei Unabhängigkeit gilt .
Sind und unabhängige Ereignisse, so gilt
Multiplikation beider Seiten mit und Ausmultiplizieren der linken Seite ergibt:
Nach Addieren des zweiten Terms der linken Seite und Anwenden der Definition für ergibt sich:
Gleichermaßen kann man zeigen, dass gilt.