Bedingte Wahrscheinlichkeit
Aus MM*Stat
Grundbegriffe
Bedingte Wahrscheinlichkeit
Gegeben seien die Ereignisse und eines Ereignisraumes .
Die Wahrscheinlichkeit für das Ereignis unter der Bedingung, dass das Ereignis eingetreten ist, bezeichnet man als die bedingte Wahrscheinlichkeit von gegeben und schreibt .
Diese bedingte Wahrscheinlichkeit ist definiert als
In analoger Weise gilt
Die bedingte Wahrscheinlichkeit lässt sich auch auf Bedingungen, die einen Durchschnitt von mehreren Ereignissen bilden, anwenden.
Gegeben seien die 3 Ereignisse und eines Ereignisraumes . Dann ist z.B.
Beispiele
Würfelwurf
Häufig ist man an der Wahrscheinlichkeit für ein bestimmtes Ereignis interessiert und verfügt über Informationen über das Eintreten von damit zusammenhängenden Ereignissen. Zur Illustration betrachte man einen Würfelwurf.
Spielerin braucht unbedingt die Augenzahl 2, um das Spiel zu gewinnen. Die Wahrscheinlichkeit für dieses Ereignis ist bekanntlich .
würfelt und verkündet ihren Gegnern: "Die Augenzahl ist gerade."
Sicherlich werden die Gegner von diese Information miteinbeziehen, wenn sie über die Wahrscheinlichkeit für eine 2 nachdenken. Formal schreibt man:
und liest: "Die Wahrscheinlichkeit für eine Zwei, gegeben eine gerade Augenzahl."
Die Lösung ist hier naheliegend. Intuitiv betrachtet man das real gewordene Ereignis als neue Grundgesamtheit, in der die Zahl 2 mit der Wahrscheinlichkeit vorkommt.
Schraubenwerkstatt
Ein Handwerker fertigt zusammen mit seinem Gesellen in Handarbeit Schrauben. Folgende Angaben beziehen sich auf die Jahresproduktion des Betriebes von 2014:
| Gesamtproduktion: | 2000 Schrauben |
| Betriebsteil 1: | 1400 Schrauben |
| (Meister) | 1162 Schrauben normgerecht |
| Betriebsteil 2: | 600 Schrauben |
| (Geselle) | 378 Schrauben normgerecht |
Da der Absatz schon länger stagniert, liegt die gesamte Jahresproduktion von 2014 in einer Kiste.
Wie hoch ist die Wahrscheinlichkeit, aus dieser Kiste eine normgerechte Schraube zu ziehen, wenn aufgrund der Kennzeichnung bekannt ist, dass diese Schraube im Betriebsteil 1 hergestellt wurde?
Zur Lösung werden folgende Ereignisse definiert:
=
=
=
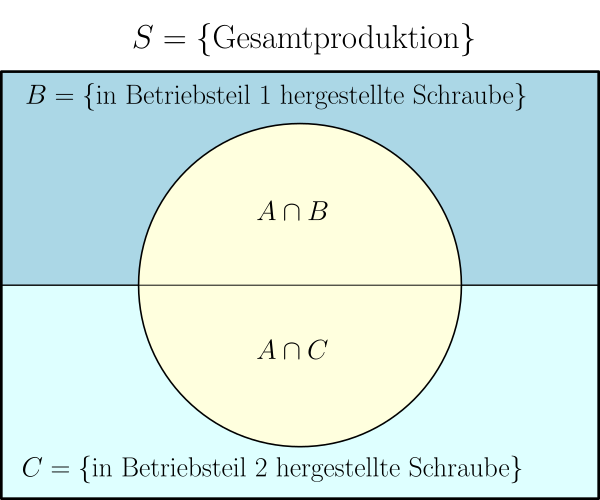
Das Venn-Diagramm veranschaulicht die Situation:
Gesucht ist . Diese bedingte Wahrscheinlichkeit ist definiert als .
Dabei bezeichnet das Ereignis Schrauben, die in Betriebsteil 1 hergestellt wurden und normgerecht sind.
Um zu erhalten, teilt man die Anzahl der Schrauben mit dieser Eigenschaft durch die Gesamtzahl:
.
ergibt sich aus dem Anteil der im Betriebsteil 1 hergestellten Schrauben an der gesamten Produktion:
.
In der Formel der bedingten Wahrscheinlichkeit kürzt sich die 2000 weg, man erhält also:
.
Die Wahrscheinlichkeit, aus der Kiste eine normgerechte Schraube zu ziehen, wenn bekannt ist, dass diese Schraube im Betriebsteil 1 hergestellt wurde, beträgt demnach 83 Prozent.
Beachten Sie, dass sich die vorgeführte Berechnung auf relative Häufigkeiten gestützt hat. Darf man also von "Wahrscheinlichkeiten" sprechen?
In diesem Fall lautet die Antwort: ja, man darf.
Denn die relativen Häufigkeiten bezogen sich auf die Grundgesamtheit (Jahresproduktion 1998) und sind daher mit Wahrscheinlichkeiten identisch.
Bei einer Ziehung aus der Produktion der Jahre 2013 und 2014 zusammen wären die obigen relativen Häufigkeiten nicht identisch mit Wahrscheinlichkeiten, wohl aber "Näherungsgrößen" dafür.