Kombinatorik/Lösungen: Unterschied zwischen den Versionen
Aus MM*Stat
(Die Seite wurde neu angelegt: „===6 aus 49=== <math>K(49,6) = </math>13 983 816<br /> ===Angebotsmöglichkeiten=== 1. Unternehmen: <math>K(6,2)= \binom{6}{2}=15</math>Kombination Preis/Me…“) |
|||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie:Aufgaben]] | |||
===6 aus 49=== | ===6 aus 49=== | ||
| Zeile 18: | Zeile 19: | ||
<math>V^{W}(2,6) = 64</math> | <math>V^{W}(2,6) = 64</math> | ||
[[File:alphabet_taktil|image]]<br /> | [[File:alphabet_taktil.gif|image]]<br /> | ||
Quelle: http://www.siljakorn.de/braille-info.shtml | Quelle: http://www.siljakorn.de/braille-info.shtml | ||
| Zeile 58: | Zeile 59: | ||
===Geburtstagsparty=== | ===Geburtstagsparty=== | ||
* | * Kombination ohne Wiederholung für <math>n = 12</math>, <math>k= 6</math>:<br> <br> | ||
K(12,6) = | |||
&= \frac{7\cdot\not 8^2\cdot\not 9 ^3\cdot\not | <math>\begin{align} | ||
&=7\ | K(12,6)=\left(\begin{array}{c} | ||
12 \\ | |||
6 | |||
\end{array}\right) &=\frac{12 !}{(12-6) ! 6 !}=\frac{12 !}{6 ! 6 !} \\ | |||
&=\frac{7 \cdot \not 8^{2} \cdot \not 9^{3} \cdot \not 10^{2} \cdot 11 \cdot \not 12^{1}}{1 \cdot \not 2 \cdot \not 3 \cdot 4 \cdot \not 5 \cdot \not 6} \\ | |||
&=7 \cdot 2 \cdot 3 \cdot 2 \cdot 11 \cdot 1=924 | |||
\end{align}</math> | |||
===Genua Wahl=== | ===Genua Wahl=== | ||
| Zeile 133: | Zeile 136: | ||
<li><p>Kombinaiton ohne Wiederholung für <math>n = 7</math> Farben:</p> | <li><p>Kombinaiton ohne Wiederholung für <math>n = 7</math> Farben:</p> | ||
<p><math>K(n,2) = \binom{7}{2}= \frac{7!}{(7-2)!2!}=\frac{7!}{5! 2!}=\frac{6\cdot7}{2}= \frac{42}{2}= 21</math></p></li> | <p><math>K(n,2) = \binom{7}{2}= \frac{7!}{(7-2)!2!}=\frac{7!}{5! 2!}=\frac{6\cdot7}{2}= \frac{42}{2}= 21</math></p></li> | ||
<li><p>Kombination mit Wiederholung für <math>n = 5</math> Farben: <math>\begin{ | <li><p>Kombination mit Wiederholung für <math>n = 5</math> Farben: <br><br> <math>\begin{align} | ||
K^{W}(n,2) = \binom{5+2-1}{2}&= \binom{6}{2}=\frac{6!}{(6-2)!2!}\\ | K^{W}(n,2) = \binom{5+2-1}{2}&= \binom{6}{2}=\frac{6!}{(6-2)!2!}\\ | ||
&=\frac{6!}{4!2!}=\frac{5\cdot6}{2}= 15 | &=\frac{6!}{4!2!}=\frac{5\cdot6}{2}= 15 | ||
\end{ | \end{align}</math></p></li></ul> | ||
===Zahlenschlösser=== | ===Zahlenschlösser=== | ||
Aktuelle Version vom 15. Juli 2020, 16:09 Uhr
6 aus 49
13 983 816
Angebotsmöglichkeiten
1. Unternehmen: Kombination Preis/Menge nicht erlaubt:
2. Unternehmen: Kombination Preis/Menge nicht erlaubt:
Insgesamt Angebotsmöglichkeiten.
Anzahl der Abweichungen
Arbeitsgänge
Blindenschrift
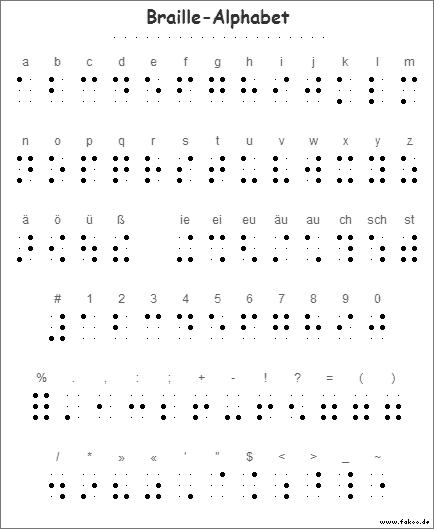
Quelle: http://www.siljakorn.de/braille-info.shtml
Bridge
Bücher
Bunte Häuser
Bunte Häuser
Camel Cup
- Unter den 22 100 Möglichkeiten sind 50 Möglichkeiten, die Testausritte mit genau einem Kamel zu machen; Möglichkeiten, die Testausritte mit 3 unterschiedliche Kamelen zu machen und folglich Möglichkeiten, die Testausritte mit zwei Kamelen zu machen.
Code-Schlösser
Computerraum-Code
Anzahl aller Codes (dritte Stelle )
Anzahl aller Codes (zweite Stelle )
Anzahl aller Codes (erste & vierte Stelle )
Einmaleins
Geburtstagsparty
- Kombination ohne Wiederholung für , :
Genua Wahl
Nein, denn Es hätte ungefähr der millionenfache Betrag des Einsatzes gezahlt werden müssen.
Geschenke für die Abteilungsleiter
Hallenschwimmbad
Hemden
Lotto Toto
Orientierungsrundgang
- Permutation :
- Permutation mit Wiederholung , :
- 60 - 43! = 36
Parkplätze
Pferdelotto
Pferderennen
Schachturnier
Schiffsignale
Schließfach
Schließfächer falls “3” bzw. “5” bzw. “7” doppelt sind.
Skatspieler
Nein, denn es gibt 64 512 240 mögliche Spiele. Der Skatspieler spielt Spiele/Jahr. Somit müsste er knapp Jahre spielen.
TEA
Unfallstation
Wagenreihungen
Wanderwege
Variation mit Wiederholung für Farben:
Kombinaiton ohne Wiederholung für Farben:
Kombination mit Wiederholung für Farben:
Zahlenschlösser
Zwei Würfel


