Additionssatz

Grundbegriffe

Additionssatz der Wahrscheinlichkeitsrechnung

Sind $A$ und $B$ zwei beliebige Ereignisse eines Zufallsexperiments, dann gilt

$P\left( A \cup B \right)=P\left( A\right) +P\left( B\right) -P\left( A \cap B\right)$,

was als Additionssatz der Wahrscheinlichkeitsrechnung bezeichnet wird.

Die Erweiterung des Additionssatzes auf drei Ereignisse $A$, $B$ und $C$ lautet:

$P\left( A \cup B \cup C\right) =P(A)+P(B)+P(C)-P \left( A \cap B\right) -P\left( A \cap C\right) -P \left( B \cap C\right) +P \left( A \cap B \cap C \right)$

Zusatzinformationen

Herleitung des Additionssatzes

• Das Ereignis $B$ kann in die beiden disjunkten Ereignisse $A \cap B$ und $\bar A \cap B$ zerlegt werden, so dass gilt

$B= (A \cap B) \cup ( \bar A \cap B)$

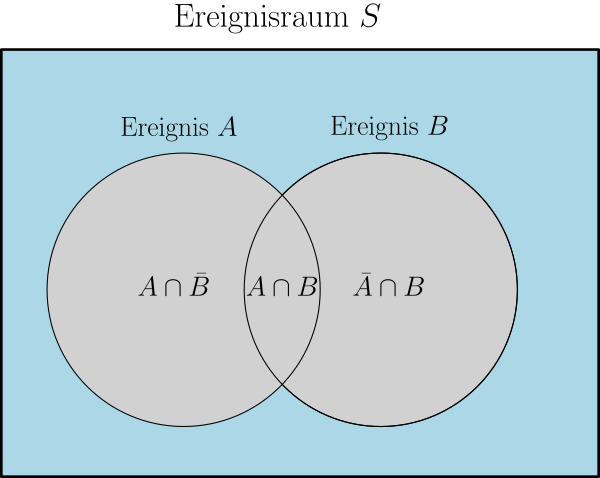
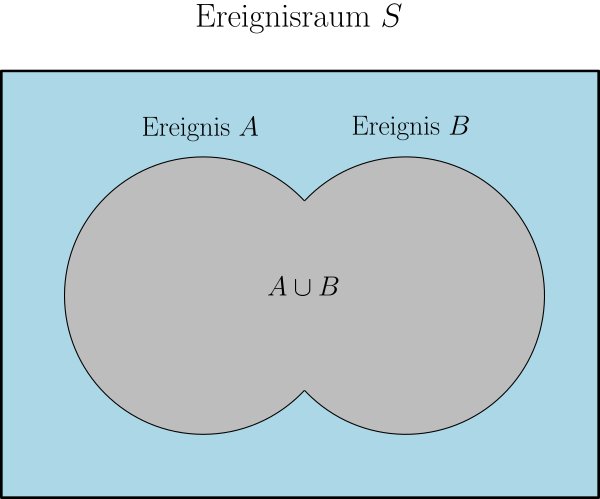
Das folgende Venn-Diagramm veranschaulicht die zugrunde liegenden Ereignisse.

Für die Wahrscheinlichkeit $P(B)$ erhält man nach Axiom 3

$P(B)=P[(A\cap B)\cup(\bar{A}\cap B)]=P(A\cap B)+P(\bar{A}\cap B)$

und nach Umformung

$P(\bar{A}\cap B)=P(B)-P(A\cap B)$

• Das Ereignis $A \cup B$ kann in die beiden disjunkten Ereignisse $A$ und $\bar A \cap B$ zerlegt werden, so dass gilt

$A \cup B = A \cup(\bar A \cap B)$

Für die Wahrscheinlichkeit $P(A \cup B)$ erhält man nach Axiom 3

$P(A \cup B) = P[A \cup(\bar A \cap B)] = P(A) + P(\bar A \cap B)$

Setzt man das Ergebnis des ersten Abschnittes für $P(\bar A \cap B)$ ein, folgt

$P(A \cup B) = P(A) + P(B) - P(A \cap B)$.

was zu beweisen war.

Beispiele

Skatspiel

Ein Skatspiel hat 32 Karten. Darin sind vier Damen und acht Herzkarten enthalten.

Gesucht sei die Wahrscheinlichkeit, aus dem unsortierten Kartenstapel zufällig eine Dame oder eine Herzkarte zu ziehen.

Für $A = {\mbox{Dame}}, \; B = {\mbox{Herzkarte}}$ und $A\cap B = {\mbox{Herzdame}}$ ergibt sich nach der klassischen Definition der Wahrscheinlichkeit:

• $P(A)=P\left( \mbox{Dame} \right) =\frac{4}{32}$
• $P(B)=P\left(\mbox{Herz}\right) =\frac{8}{32}$
• $P(A\cap B)=P(\mbox{Herzdame}) =\frac{1}{32}$

Gesucht ist die Wahrscheinlichkeit $P(A\cup B)$

Nach dem Additionssatz ergibt sich:

$P\left( A\cup B\right)$	$=P\left(A\right) +P\left( B\right) -P\left( A\cap B\right)$
	$= \frac{4}{32} + \frac{8}{32}- \frac{1}{32}= \frac{11}{32}$

Die Wahrscheinlichkeit, aus dem unsortierten Kartenstapel zufällig eine Dame oder eine Herzkarte zu ziehen, beträgt $\frac{11}{32}$.