تحليل الانحدار الأحادي البعد

$y_{i}={\widehat {y_{i}}}+{\widehat {u_{i}}}$ لكل مشاهدة i

حللنا القيم المشاهدة $y_{i}$ لجزئين:

تابع الانحدار المقدر ${\widehat {y_{i}}}={\widehat {E(y_{i}\vert x_{i})}}$ بمعنى: تقدير المتوسط الشرطي.

والبواقي المقدرة ${\widehat {u_{i}}}$.

$\sum _{i=1}^{n}{(y_{i}-{\widehat {y_{i}}})}({\widehat {y_{i}}}-{\bar {y}})=0$

يحفز القارئ لبرهان هذا الاستعمال المربعات الأقل أولا أو الشرط فوق مع التعريف ${{\widehat {y_{i}}}.}$

نقسم طرفي المعادلة الثانية على n ينتج لدينا :

${\frac {\sum _{i}^{n}{(y_{i}-{\bar {y}})}^{2}}{n}}={\frac {\sum _{i=1}^{n}{(y_{i}-{\widehat {y_{i}}})}^{2}}{n}}+{\frac {\sum _{i=1}^{n}{({\widehat {y_{i}}}-{\bar {y}})}^{2}}{n}}$

${\frac {\sum _{i}^{n}{(y_{i}-{\bar {y}})}^{2}}{n}}={\frac {\sum _{i=1}^{n}{\hat {u_{i}}}^{2}}{n}}{\frac {\sum _{i=1}^{n}{({\widehat {y_{i}}}-{\bar {y}})}^{2}}{n}}$

${S_{y}}^{2}={S_{\hat {u}}}^{2}+{S_{\hat {y}}}^{2}$

تباين العينة الاجمالي $Y$ يساوي الى مجموع تباين العينة للبواقي المقدرة ( الجزء غير المفسر لتباين $Y$ )وجزء تباين $Y$ الذي يفسر بواسطة تابع الانحدار. ( تابع العينة لتابع الانحدار).

• الجزء الأكبر من تباين العينة $y$

يفسر بواسطة النموذج ${S_{\hat {y}}}^{2})$ أفضل مطابقة لخط الانحدار.

• من جهة أخرى كبر تباين البواقي ${\hat {{S_{u}}^{2}}}$

كنسبة مئوية لتباين العينة $y$ بشكل بديل كبر التأثيرات الخارجية غير المفسرة بواسطة تابع الانحدار يطابق أسؤا تابع انحدار.

معامل التحديد:

يعرف معامل التحديد كنسبة تباين $Y$ المفسر بواسطة تابع الانحدار والتباين الاجمالي $Y$ ذلك يعني تعرض نسبة تباين العينة $y$ المفسرة بواسطة تابع الانحدار المقدر.

$R_{yx}^{2}={\frac {\sum _{i=1}^{n}{({\widehat {y_{i}}}-{\bar {y}})}^{2}}{\sum _{i=1}^{n}{(y_{i}-{\bar {y}})}^{2}}}={\frac {{S_{\hat {y}}}^{2}}{{S_{y}}^{2}}}$

كطريقة بديلة لحساب معامل التحديد:

$R_{yx}^{2}={\frac {{[\sum _{i=1}^{n}(y_{i}-{\bar {y}})(x_{i}-{\bar {x}})]}^{2}}{\sum _{i=1}^{n}{(y_{i}-{\bar {y}})}^{2}\sum _{i=1}^{n}{(x_{i}-{\bar {x}})}^{2}}}={\frac {{S_{xy}}^{2}}{{S_{y}}^{2}{S_{x}}^{2}}}$

$R_{xy}^{2}={\frac {{(n\sum _{i=1}^{n}x_{i}y_{i}-\sum _{i=1}^{n}x_{i}\sum _{i=1}^{n}y_{i})}^{2}}{[n\sum _{i=1}^{n}{x_{i}}^{2}-{(\sum _{i=1}^{n}x_{i})}^{2}][n\sum _{i=1}^{n}{y_{i}}^{2}-{(\sum _{i=1}^{n}y_{i})}^{2}]}}$

الخواص:

• يقع معامل التحديد دائما في المجال التالي: $0\leq R_{yx}^{2}\leq 1$

ارتفاع قيمة معامل التحديد ذلك يعني أفضل تابع انحدار يشرح القيم المشاهدة.

اذا كل القيم المشاهدة تتوضع على خط الانحدار معامل التحديد يساوي للواحد سيشرح التباين الاجمالي $Y$ بواسطة المتغير $X$.

$Y$ ترتبط بشكل تام وخطي مع $X$

اذا معامل التحديد مساوي للصفر التباين الاجمالي $Y$ متطابق مع التباين غير المفسر (تباين البواقي) المتغير العشوائي $X$ لا تأثير له على $Y$

• $R_{xy}^{2}=R_{yx}^{2}$

بشكل متناظر : مطابقة انحدار $y$ على $x$ متماثلة مع مطابقة انحدار $x$ على $y$.

• لأجل تابع الانحدار الخطي يطابق معامل التحديد لمربع معامل الارتباط

$R_{yx}^{2}=r_{yx}^{2}$.

مثال:

لأجل الاستقلال الموصوف سابقا بين وقت العمل ومخرجات الانتاج. معامل الارتباط البسيط ومعامل التحديد هو:

${r_{yx}}^{2}=0,9977$

${R_{yx}}^{2}=0,9954$

تابع الانحدار غير الخطي ذو البعد الواحد :

مثال:

$n=8$ المدن المقارنة

$X$ عدد وسائط النقل العامة الموزعة لمواطني المدينة عند بداية تحليل الفترة الزمنية.

$Y$ الزيادة في أعداد المواطنين المستعملين لوسائط النقل العامة خلال تحليل الفترة الزمنية.

المدينة $i$	الزيادة $Y$ (in 1000)	وسائط النقل العامة $X$ (in 1000)
1	0,60	80
2	6,70	220
3	5,30	140
4	4,00	120
5	6,55	180
6	2,15	100
7	6,60	200
8	5,75	160

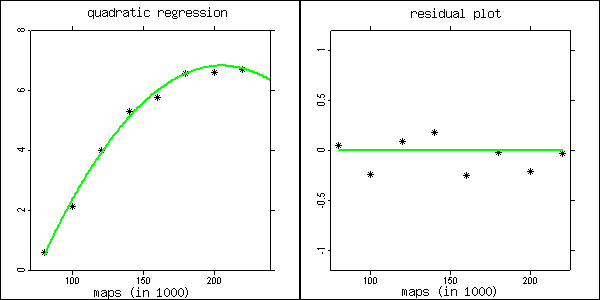
الانحدار الخطي :

${\widehat {y_{i}}}={\widehat {b_{0}}}+{\widehat {b_{1}}}x_{i}=-1,82+0,0435x_{i}$

${R_{yx}}^{2}=0,875$

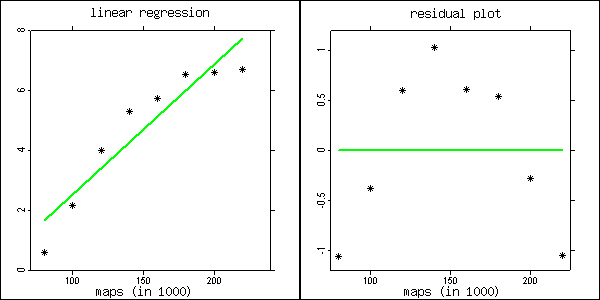
نرى من الأشكال البيانية أن البواقي المقدرة لا تتوزع بشكل عشوائي حول الصفر لكن حصلنا على نماذج غير خطية نوعا ما حينئذ من المفيد استعمال نموذج الانحدار غير الخطي بدلا من النموذج الخطي.

الانحدار التربيعي

${\widehat {y_{i}}}={\widehat {b_{0}}}+{\widehat {b_{1}}}x_{i}+{{\widehat {b_{2}}}x_{i}}^{2}=-10,03+0,1642x_{i}-0,0004{x_{i}}^{2}$

${R_{yx}}^{2}=0,995$