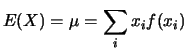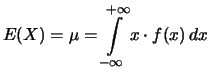الفرق بين المراجعتين لصفحة: «العناصر»

من MM*Stat Arabisch

اذهب إلى: تصفح, ابحث
لا ملخص تعديل
لا ملخص تعديل
 
سطر ١: سطر ١:
<math> X</math> بواسطة <math> E(X)</math>  أو  <math> \mu ,</math> المطابقة [[ للوسط الحسابي]] [[للتوزيع التكراري]] التجريبي.
[[ العناصر]],  [[ مثال2: المتغير العشوائي المستمر  ]], [[مثال المتغير العشوائي المنقطع  ]]


القيمة المتوقعة  هي قيمة المتوسط  والمتوقع  الحصول عليها  كنتيجة [[التجربة ]], باعادة  التجربة  عدة مرات , القيمة  المتوقعة <math> E(X)</math> هو العدد الذي تم الحصول  عليه  كمتوسط  كل نتائج  التجربة.
 
 
 
 
[[صورة:H100.gif]]  ''' 5.4  العناصر  '''
 
 
 
 
يوصف أي  [[متغير عشوائي]]  [[بكثافته]] الاحتمالية  و [[توابع توزيعه]], على أية حال  توصف  بعض السمات  المهمة  [[للتوزيع  الاحتمالي]]  بواسطة عدد صغير من العناصر. 
العناصر الأكثر  الأهمية  هي عناصر النزعة المركزية  للمتغير العشوائي.
 
 
'''القيمة المتوقعة '''
 
 
ترمز القيمة  المتوقعة  للمتغير العشوائي [[صورة:Mmengjavaimg4.gif]] بواسطة [[صورة:Mmengjavaimg924.gif]]  أو  [[صورة:Mmengjavaimg925.gif]]  المطابقة [[ للوسط الحسابي]]  [[للتوزيع التكراري]] التجريبي.
 
القيمة المتوقعة  هي قيمة المتوسط  والمتوقع  الحصول عليها  كنتيجة [[التجربة ]], باعادة  التجربة  عدة مرات , القيمة  المتوقعة [[صورة:Mmengjavaimg924.gif]] هو العدد الذي تم الحصول  عليه  كمتوسط  كل نتائج  التجربة.




التعريف:  
التعريف:  


نعتبر المتغير العشوائي <math> X</math> مع النتائج  <math> x_{i}</math> و الاحتمالات  المطابقة <math> f(x_{i})</math>.  عندئذ يعرف التعبير:
نعتبر المتغير العشوائي [[المنقطع]] [[صورة:Mmengjavaimg4.gif]] مع النتائج  [[صورة:Mmengjavaimg125.gif]] و الاحتمالات  المطابقة [[صورة:Mmengjavaimg843.gif]].  عندئذ يعرف التعبير:






<math> E(X)=\mu =\sum\limits_{i}x_{i}f(x_{i})
[[صورة:Mmengjavaimg926.gif]]
</math>






بالقيمة  المتوقعة  للمتغير العشوائي <math> X</math> .
بالقيمة  المتوقعة  للمتغير العشوائي [[صورة:Mmengjavaimg4.gif]] .




لأجل  المتغير العشوائي [[المستمر]] <math> X</math> مع  الكثافة الاحتمالية <math> f(x)</math> نعرف القيمة  المتوقعة  كالتالي:
لأجل  المتغير العشوائي [[المستمر]] [[صورة:Mmengjavaimg4.gif]] مع  الكثافة الاحتمالية [[صورة:Mmengjavaimg290.gif]] نعرف القيمة  المتوقعة  كالتالي:






<math> E(X)=\mu =\int\limits_{-\infty }^{+\infty }x\cdot f(x)\,dx
[[صورة:Mmengjavaimg927.gif]]
</math>




سطر ٣١: سطر ٤٧:




نفرض <math> X</math> و <math> Y</math> متغيرين عشوائيين  مع قيمهم المتوقعة <math> E(X)</math> و <math> E(Y)</math> عندئذ :
نفرض [[صورة:Mmengjavaimg4.gif]] و [[صورة:Mmengjavaimg6.gif]] متغيرين عشوائيين  مع قيمهم المتوقعة [[صورة:Mmengjavaimg924.gif]] و [[صورة:Mmengjavaimg928.gif]] عندئذ :






<LI> لأجل <math> Y = a+bX</math> مع أي  <math> a,b</math>
<LI> لأجل [[صورة:Mmengjavaimg929.gif]] مع أي  [[صورة:Mmengjavaimg930.gif]]
</LI>
</LI>




<math> E(Y) = E(a+bX) = a + bE(X)</math>
[[صورة:Mmengjavaimg931.gif]]






<LI>  وبالنسبة  <math> Z=X+Y</math>
<LI>  وبالنسبة  [[صورة:Mmengjavaimg932.gif]]
</LI>
</LI>




<math> E(Z) = E(X + Y) = E(X) + E(Y)</math>
[[صورة:Mmengjavaimg933.gif]]






<LI>لأجل <math> X,Y</math> متغيرين عشوائيين  مستقلين
<LI>لأجل [[صورة:Mmengjavaimg934.gif]] متغيرين عشوائيين  مستقلين
</LI>
</LI>




<math> E(XY) = E(X)E(Y)</math>
[[صورة:Mmengjavaimg935.gif]]




سطر ٦٤: سطر ٨٠:
تعريف :  
تعريف :  


يرمز التباين عادة  بواسطة <math> Var(X)</math> أو <math> \sigma ^{2},</math> ويعرف  بالقيمة المتوقعة  للانحرافات  المربعة  بين المتغير العشوائي  وقيمته المتوقعة :
يرمز التباين عادة  بواسطة [[صورة:Mmengjavaimg936.gif]] أو [[صورة:Mmengjavaimg937.gif]] ويعرف  بالقيمة المتوقعة  للانحرافات  المربعة  بين المتغير العشوائي  وقيمته المتوقعة :




<math> Var(X) = E[(X-E(X))^2] = E(X^2) = [E(X)]^2
[[صورة:Mmengjavaimg938.gif]]
</math>


   
   
سطر ٧٤: سطر ٨٩:




<math> Var(X)=\sigma ^{2}=\sum\limits_{i}[x_{i}-E(X)]^{2}\cdot
[[صورة:Mmengjavaimg939.gif]]
f(x_{i})=\sum\limits_{i}x_{i}^{2}f(x_{i})-[E(X)]^{2}
</math>


   
   
سطر ٨٤: سطر ٩٧:




<math> Var(X)=\sigma ^{2}=\int\limits_{-\infty }^{+\infty }[x-E(X)]^{2}\cdot
[[صورة:Mmengjavaimg940.gif]]
f(x)\,dx=\int\limits_{-\infty }^{+\infty }x^{2}f(x)\,dx-[E(X)]^{2}
</math>




سطر ٩٤: سطر ١٠٥:




نفرض <math> X</math> و <math> Y</math> متغيرين  عشوائيين  مع تبايناتهم <math> Var(X)</math> و <math> Var(Y)</math> عندئذ :
نفرض [[صورة:Mmengjavaimg4.gif]] و [[صورة:Mmengjavaimg6.gif]] متغيرين  عشوائيين  مع تبايناتهم [[صورة:Mmengjavaimg936.gif]] و [[صورة:Mmengjavaimg941.gif]] عندئذ :




<LI>لأجل <math> Y = a+bX</math> حيث  <math> a</math> و <math> b</math> ثوابت  
<LI>لأجل [[صورة:Mmengjavaimg929.gif]] حيث  [[صورة:Mmengjavaimg378.gif]] و [[صورة:Mmengjavaimg911.gif]] ثوابت  
</LI>
</LI>




<math> Var(Y)=Var(a+bX)=b^{2}Var(X)</math>
[[صورة:Mmengjavaimg942.gif]]




<LI>  وأيضا اذا كان <math> X,Y</math> متغيرات عشوائية مستقلة و <math> Z=X+Y</math>
<LI>  وأيضا اذا كان [[صورة:Mmengjavaimg934.gif]] متغيرات عشوائية مستقلة و [[صورة:Mmengjavaimg932.gif]]
</LI>
</LI>




<math> Var(Z)=Var(X)+Var(Y)</math>
[[صورة:Mmengjavaimg943.gif]]






<math> \sigma _{Z}=\sigma _{X+Y}=
[[صورة:Mmengjavaimg944.gif]]
\sqrt{\sigma _{X}^{2}+\sigma _{Y}^{2}}
</math>




سطر ١٢١: سطر ١٣٠:




يرمز الانحراف المعياري <math> \sigma </math> بالجذر التربيعي  للتباين  الذي  يلخص  انتشار التوزيع, تدل القيم  الكبيرة  لمتوسط الانحراف المعياري  بأن المتغير العشوائي  <math> X</math> تجاوز  بشكل كبير  حول القيمة المتوقعة.تشير  القيم  الصغيرة  للانحراف  المعياري  بأن  قيم  <math> X</math> ستتركز  حول  القيمة المتوقعة.  
يرمز الانحراف المعياري [[صورة:Mmengjavaimg945.gif]] بالجذر التربيعي  للتباين  الذي  يلخص  انتشار التوزيع, تدل القيم  الكبيرة  لمتوسط الانحراف المعياري  بأن المتغير العشوائي  [[صورة:Mmengjavaimg4.gif]] تجاوز  بشكل كبير  حول القيمة المتوقعة.تشير  القيم  الصغيرة  للانحراف  المعياري  بأن  قيم  [[صورة:Mmengjavaimg4.gif]] ستتركز  حول  القيمة المتوقعة.  




سطر ١٣٣: سطر ١٤٢:




<math> Z=\frac{X-E(X)}{\sigma _{X}}
[[صورة:Mmengjavaimg946.gif]]
</math>


القيمة المتوقعة <math> E(Z)=0</math> والتباين <math> Var(Z)=1</math> .
القيمة المتوقعة [[صورة:Mmengjavaimg947.gif]] والتباين [[صورة:Mmengjavaimg948.gif]] .




سطر ١٤٨: سطر ١٥٦:




تبنى المتباينة على المجال: <math> [\mu -k\cdot \sigma ;\mu +k\cdot
تبنى المتباينة على المجال: [[صورة:Mmengjavaimg949.gif]] الذي  يتمركز  حول [[صورة:Mmengjavaimg950.gif]]
\sigma ]</math> الذي  يتمركز  حول <math> \mu </math>


   
   
التعريف :  
التعريف :  


نعتبر  المتغير  العشوائي  <math> X</math> مع  القيمة المتوقعة <math> \mu </math> والتباين  <math> \sigma </math>   عندئذ  لأجل أي <math> k > 0</math> لدينا
نعتبر  المتغير  العشوائي  [[صورة:Mmengjavaimg4.gif]] مع  القيمة المتوقعة [[صورة:Mmengjavaimg950.gif]] والتباين  [[صورة:Mmengjavaimg945.gif]]   عندئذ  لأجل أي [[صورة:Mmengjavaimg951.gif]] لدينا




<math> P(\mu - k \cdot \sigma \leq X \leq \mu + k \cdot \sigma) \geq 1 - \frac{1}{
[[صورة:Mmengjavaimg952.gif]]
k^2}
</math>






نرمز <math> k \cdot \sigma = a</math> نحصل:  
نرمز [[صورة:Mmengjavaimg953.gif]] نحصل:  






<math> P(\mu - a \leq X \leq \mu + a) \geq 1 - \frac{\sigma^2}{k^2}
[[صورة:Mmengjavaimg954.gif]]
</math>






نستعمل التباين  للحصول  على حد [[الحادث المكمل ]] بأن المتغير العشوائي <math> X</math> يسقط  خارج  المجال, <math> \{\vert X-\mu \vert>k\cdot \sigma \}</math>
نستعمل التباين  للحصول  على حد [[الحادث المكمل ]] بأن المتغير العشوائي [[صورة:Mmengjavaimg4.gif]] يسقط  خارج  المجال, [[صورة:Mmengjavaimg955.gif]]




<math> P(\vert X-\mu \vert>k\cdot \sigma )<1/k^{2}
[[صورة:Mmengjavaimg956.gif]]
</math>




ولأجل <math> k \cdot \sigma = a</math>
ولأجل [[صورة:Mmengjavaimg953.gif]]






<math> </math><math> P(\vert X-\mu \vert>a)<\sigma ^{2}/a^{2}</math>
[[صورة:Mmengjavaimg903.gif]][[صورة:Mmengjavaimg957.gif]]




نلاحظ  بأن الاحتمالات الصحيحة <math> \{\vert X-\mu \vert<k\cdot \sigma \}</math> و <math> \{\vert X-\mu \vert\leq k\cdot \sigma \}</math> تعتمد  على التوزيع المحدد <math> X</math>.
نلاحظ  بأن الاحتمالات الصحيحة [[صورة:Mmengjavaimg958.gif]] و [[صورة:Mmengjavaimg959.gif]] تعتمد  على التوزيع المحدد [[صورة:Mmengjavaimg4.gif]].

المراجعة الحالية بتاريخ ١٧:٤٦، ٣١ يوليو ٢٠٢٠

العناصر, مثال2: المتغير العشوائي المستمر , مثال المتغير العشوائي المنقطع



H100.gif 5.4 العناصر



يوصف أي متغير عشوائي بكثافته الاحتمالية و توابع توزيعه, على أية حال توصف بعض السمات المهمة للتوزيع الاحتمالي بواسطة عدد صغير من العناصر. العناصر الأكثر الأهمية هي عناصر النزعة المركزية للمتغير العشوائي.


القيمة المتوقعة


ترمز القيمة المتوقعة للمتغير العشوائي Mmengjavaimg4.gif بواسطة Mmengjavaimg924.gif أو Mmengjavaimg925.gif المطابقة للوسط الحسابي للتوزيع التكراري التجريبي.

القيمة المتوقعة هي قيمة المتوسط والمتوقع الحصول عليها كنتيجة التجربة , باعادة التجربة عدة مرات , القيمة المتوقعة Mmengjavaimg924.gif هو العدد الذي تم الحصول عليه كمتوسط كل نتائج التجربة.


التعريف:

نعتبر المتغير العشوائي المنقطع Mmengjavaimg4.gif مع النتائج Mmengjavaimg125.gif و الاحتمالات المطابقة Mmengjavaimg843.gif. عندئذ يعرف التعبير:


Mmengjavaimg926.gif


بالقيمة المتوقعة للمتغير العشوائي Mmengjavaimg4.gif .


لأجل المتغير العشوائي المستمر Mmengjavaimg4.gif مع الكثافة الاحتمالية Mmengjavaimg290.gif نعرف القيمة المتوقعة كالتالي:


Mmengjavaimg927.gif



خواص القيمة المتوقعة:


نفرض Mmengjavaimg4.gif و Mmengjavaimg6.gif متغيرين عشوائيين مع قيمهم المتوقعة Mmengjavaimg924.gif و Mmengjavaimg928.gif عندئذ :


  • لأجل Mmengjavaimg929.gif مع أي Mmengjavaimg930.gif

    • Mmengjavaimg931.gif

  • وبالنسبة Mmengjavaimg932.gif

    • Mmengjavaimg933.gif

  • لأجل Mmengjavaimg934.gif متغيرين عشوائيين مستقلين

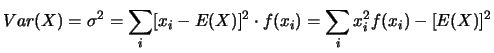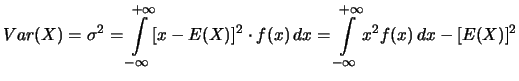    • Mmengjavaimg935.gif التباين تعريف : يرمز التباين عادة بواسطة Mmengjavaimg936.gif أو Mmengjavaimg937.gif ويعرف بالقيمة المتوقعة للانحرافات المربعة بين المتغير العشوائي وقيمته المتوقعة : Mmengjavaimg938.gif وبالنسبة للمتغير العشوائي المنقطع  : Mmengjavaimg939.gif وكذلك بالنسبة للمتغير العشوائي المستمر يعرف التباين كالتالي : Mmengjavaimg940.gif خواص التباين : نفرض Mmengjavaimg4.gif و Mmengjavaimg6.gif متغيرين عشوائيين مع تبايناتهم Mmengjavaimg936.gif و Mmengjavaimg941.gif عندئذ :

  • لأجل Mmengjavaimg929.gif حيث Mmengjavaimg378.gif و Mmengjavaimg911.gif ثوابت

    • Mmengjavaimg942.gif

  • وأيضا اذا كان Mmengjavaimg934.gif متغيرات عشوائية مستقلة و Mmengjavaimg932.gif

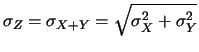    • Mmengjavaimg943.gif Mmengjavaimg944.gif الانحراف المعياري يرمز الانحراف المعياري Mmengjavaimg945.gif بالجذر التربيعي للتباين الذي يلخص انتشار التوزيع, تدل القيم الكبيرة لمتوسط الانحراف المعياري بأن المتغير العشوائي Mmengjavaimg4.gif تجاوز بشكل كبير حول القيمة المتوقعة.تشير القيم الصغيرة للانحراف المعياري بأن قيم Mmengjavaimg4.gif ستتركز حول القيمة المتوقعة. الدالة المعيارية من المفيد تحويل المتغير العشوائي لنحصل على التوزيع غير المتعلق بأي من العناصر (المجهولة). 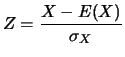وبالتالي نحصل على المتغير العشوائي المعياري: Mmengjavaimg946.gif القيمة المتوقعة Mmengjavaimg947.gif والتباين Mmengjavaimg948.gif . متباينة تشيببتشف تزود متباينة تشيببتشف حد الاحتمال بأن المتغير العشوائي يقع ضمن المجال حول قيمته المتوقعة. يتطلب هذا التوزيع معرفة القيمة المتوقعة والتباين للتوزيع , لا نعرف التوزيع بحد ذاته . 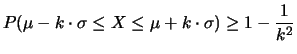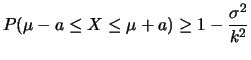تبنى المتباينة على المجال: Mmengjavaimg949.gif الذي يتمركز حول Mmengjavaimg950.gif التعريف : نعتبر المتغير العشوائي Mmengjavaimg4.gif مع القيمة المتوقعة Mmengjavaimg950.gif والتباين Mmengjavaimg945.gif عندئذ لأجل أي Mmengjavaimg951.gif لدينا Mmengjavaimg952.gif نرمز Mmengjavaimg953.gif نحصل: Mmengjavaimg954.gif نستعمل التباين للحصول على حد الحادث المكمل بأن المتغير العشوائي Mmengjavaimg4.gif يسقط خارج المجال, Mmengjavaimg955.gif Mmengjavaimg956.gif ولأجل Mmengjavaimg953.gif Mmengjavaimg903.gifMmengjavaimg957.gif نلاحظ بأن الاحتمالات الصحيحة Mmengjavaimg958.gif و Mmengjavaimg959.gif تعتمد على التوزيع المحدد Mmengjavaimg4.gif.

    مجلوبة من «https://wikis.hu-berlin.de/mmara/w/index.php?title=العناصر&oldid=2413»