|
|
| سطر ١: |
سطر ١: |
| [[اختبار المتوسطات الطبيعية]],[[مثال لاختبار متوسط المجتمع]],[[اختبار متوسط المجتمع ]]
| | <math> \N\left( \mu =0,\,\sigma =1\right) </math>. |
| | |
| | |
| | |
| [[صورة:H100.gif]] '''9.2 اختبار المتوسطات الطبيعية'''
| |
| | |
| | |
| | |
| | |
| يهتم المرء في العديد من التطبيقات بمتوسط توزيع المجتمع لمتغير عشوائي , تخبرنا نظرية التقدير
| |
| | |
| الاحصائية ما هو التقدير الأفضل لتوقع شكل التوزيع المعطى ولا يساعدنا في تقييم المتوسط المقدر,
| |
| | |
| يحسب المتوسط من العينة ذات الحجم n=5 وسيكون عدد مفرد على أساس حجم العينة من n=5000
| |
| | |
| بالاضافة, يدلنا قانون الأعداد الكبيرة للاعتقاد أن التقدير أكثر تمثيلا من الأول المبني على متوسط
| |
| | |
| العينة (مثال : الوسط الحسابي) للعينات الكبيرة يقترب لمتوسط المجتمع من العينات الصغيرة. ذلك يعني
| |
| | |
| تحسب متوسطات العينة من العينات الكبيرة بشكل أكثر دلالة احصائيا.
| |
| | |
| تقترب طريقة تحديد المتوسط لعنصر المجتمع ليحسب الخطأ المعياري تحت (هنا المتوسط)
| |
| | |
| بمعنى الجذر التربيعي لمتوسط الانحرافات المربعة المقدرة [[للمقدر]] عن عنصر المجتمع, متوسط العينة الحالي
| |
| | |
| لعينة معطاة سيشترك مع انحرافها المعياري لتحديد المجال.
| |
| | |
| الأن نفرض بعض الاجراءات العملية , القيمة للوسط النظري المشتقة من فروض النظرية أو تحليل
| |
| | |
| البيانات, اذا القيمة النظرية تقرب لمتوسط العينة , بشكل عملي ضمن المجال المحدد حول متوسط العينة.
| |
| | |
| من الأفضل افتراض متوسط المجتمع الصحيح , عندئذ اذا له أبعد قيمة , لكن الأن كيف بعد متوسط
| |
| | |
| العينة عن متوسط المجتمع النظري لتقييم بعبارات احتمالية ملائمة لاتخاذ القرارات على أساس مفهوم
| |
| | |
| خطأ <math>\alpha</math> ؟ بكلمات أخرى : كيف يمكننا بناء الاختبار الاحصائي لمتوسط المتغير العشوائي؟
| |
| | |
| | |
| هدفنا اختيار القيمة المحددة للتوقع <math>E(X) = \mu</math> لتوزيع المجتمع وبياناتنا عشوائية مسحوبة من العينة ذات الحجم n.
| |
| | |
| من الناحية النظرية بواسطة [[متغيرات العينة]] <math>X_{1},\ldots ,X_{n}</math> ونريد بناء قرار الاختبار عند مستوى الدلالة <math>\alpha</math>
| |
| | |
| | |
| | |
| [[صورة:H100.gif]] ''' الفرضيات'''
| |
| | |
| | |
| نعين الفرضيات للاختبارات الثنائية والأحادية الجانب:
| |
| | |
| | |
| الاختبار الثنائي الجانب:
| |
| | |
| | |
| <math>H_{0}: \mu =\mu _{0},\quad H_{1}: \mu \neq \mu _{0}</math>
| |
| | |
| | |
| الاختبار الأحادي الجانب الأيمن :
| |
| | |
| | |
| <math>H_{0}:\mu \leq \mu _{0},\quad H_{1}: \mu >\mu _{0}</math>
| |
| | |
| | |
| الاختبار الأحادي الجانب الأيسر:
| |
| | |
| | |
| <math>H_{0}: \mu \geq \mu _{0},\quad H_{1}: \mu <\mu _{0}</math>
| |
| | |
| | |
| لدينا من اختبارات الفرضيات الاحصائية الأحادية الجانب, مشكلة التقدير العلمي ليصبح صالح كالفرضيات البديلة <math>H_{1}</math> بدلا من الفرضيات الصفرية <math>H_{0}</math>
| |
| | |
| ذلك يعني, يحاول الباحثون احصائيا انكار صحة الفرضيات المختبرة والتي لا تحمل لمستوى الدلالة المعينة <math>\alpha</math>.
| |
| | |
| هذا بسبب طبيعة مستوى الدلالة لاحظنا سابقا : رفض الفرضية الصفرية عند مستوى دلالة معينة يعتمد فقط على احتمال كونها خاطئة وأكبر من <math>\alpha</math>
| |
| | |
| عندما 0,01 أو 0,05 مختارة بشكل صغير , يحاول الشخص السيطرة على خطأ <math>\alpha</math> لترتيب
| |
| | |
| الوضع غير المراد هذا يصنع معنى اذا اعتقد المرء ببعض التطبيقات المطبقة في هذا المفهوم لاختبار عقار
| |
| | |
| جديد بأثاره الجانبية الضارة, على سبيل المثال نقبل المفهوم بأن التأثيرات الجانبية لا تذكر
| |
| | |
| ونستند في هذا المفهوم للعلاقة (المجهولة ) بين <math>\alpha</math>و <math>\beta</math>
| |
| | |
| | |
| | |
| [[صورة:H100.gif]] ''' الاختبار الاحصائي , توزيعه ومجالات القرار المشتقة'''
| |
| | |
| | |
| نحتاج لتلخيص المعلومات في العينة العشوائية والتي تتطلب عمل العبارات الاحتمالية حول خواص التوزيع المجهول.
| |
| | |
| (في الحالة الأن , متوسط المجتمع ) للاختبارات العددية , [[مقدر العنصر]] , نحتاج مسبقا لاظهار الوسط الحسابي:
| |
| | |
| | |
| <math>\bar{X}=\frac{1}{n}\sum_{i=1}^{n}\,X_{i}</math>
| |
| | |
| | |
| والمقبول احصائيا , مقدر النقطة لمتوسط المجتمع المجهول بمعنى التوقع المجهول <math>E(X) = \mu</math> بشكل عملي غير متحيز وفعال.
| |
|
| |
| يعطى التباين والانحراف المعياري الى <math>\bar{X}</math> المحسوب من [[العينة العشوائية]] بواسطة:
| |
| | |
| | |
| <math>Var\left( \bar{X}\right) =\sigma ^{2}\left( \bar{X}\right)=\frac{\sigma _{X}^{2}}{n}</math>
| |
| | |
| <math>\sigma \left( \overline{X}\right) =\frac{\sigma }{\sqrt{n}}</math>
| |
| | |
|
| |
| سنبني اختبارنا الاحصائي حول متوسط العينة <math>\bar{X}</math>, لاشتقاق مجالات الرفض وعدم
| |
| | |
| الرفض المطابقة لمستوى الدلالة المعطاة, نحتاج لعمل افتراض توزيع متوسط العينة اما:
| |
| | |
| *المتغير العشوائي <math>X</math> له توزيع طبيعي يعني التوزيع الطبيعي الى <math>\bar{X}</math> أو
| |
| | |
| *<math>n</math> كبيرة بشكل كافي لتبرير تطبيق [[نظرية الحد المركزية]] اذا:[[ متغيرات العينة]] <math>X_{i}</math> هي توزيعات مستقلة ومتماثلة مع المتوسط والتباين المحدد.
| |
| | |
| <math>\bar{X}</math> تقرب للتوزيع الطبيعي في هذه الحالة سيقرب اختبارنا للواحد
| |
| لذلك نسلم بما يلي :
| |
| | |
| | |
| <math>\bar{X}</math> له التوزيع الطبيعي (على الأقل تقريبي) مع التوقع <math>E(\bar{X}) = \mu_{0}</math> والتباين <math>\sigma^{2}(\bar{X}) = \sigma^{2}/n</math>
| |
| | |
| لهذا توزيع [[المقدر]] لمتوسط المجتمع <math> \mu</math> يعتمد على العنصر المجهول نسعى لاختبار <math> \mu</math> , الطريق الوحيد للتغلب على هذا التصميم تحديد القيمة العددية الى <math> \mu</math>
| |
| | |
| القيمة الدنيا لتأخذ قيمة الحد في الفرضية الصفرية بمعنى تقسم القيمة مجالات العنصر لأجل <math>H_{0}</math> و <math>H_{1}</math>.
| |
| | |
| اذا تذكرنا مفهوم رفض الفرضية الصفرية لترتيب عدم رفض [[الفرضية البديلة]] , بناء على القرار للتوزيع المفترض لاختبارنا الاحصائي مع العنصر <math>\mu_{0}</math>.
| |
| | |
| يمكننا من اختبار <math>\mu</math> , بازالة عدم الدقة في [[تابع التوزيع]] , نلاحظ في الاختبار الثنائي الجانب <math>\mu_{0}</math>. والتي تصنع فضاء كامل العنصر للفرضية الصفرية , في
| |
| الاختبار الأحادي الجانب تكون القيمة الحدية.
| |
|
| |
| دعنا نضع افتراضنا ومجموعة التوقع الى <math>X</math> بمعنى: <math>\mu=\mu_{0}</math>
| |
| | |
| نعطي الفرضية الصفرية <math>H_{0}: \mu= \mu_{0}</math> صحيحة, بالتوالي <math>\mu</math> تساوي القيمة الحدية للفرضية الصفرية للاختبار الأحادي الجانب .
| |
| | |
| نكتب <math>\bar{X}</math> كتوزيع طبيعي (على الأقل تقريبي) مع التوقع <math>E(\bar{X})=\mu_{0}</math> والتباين <math>\sigma^{2}(\bar{X})=\sigma^{2}/n</math>
| |
| | |
| أو باستعمال الترميز العام لتوابع التوزيع الطبيعي:
| |
| | |
| | |
| <math>\overline{X}{\underline{ \mbox{ }H_{0}}}{\sim }\N\left( \mu_{0};\;\sigma/\sqrt{n}\right)</math>
| |
| | |
| | |
| حتى الأن نركز على العنصر <math>\mu</math> لكن ماذا بخصوص العزم المركزي الثاني الذي يحدد التوزيع الطبيعي , تباين المتغير العشوائي (وبالتالي الانحراف المعياري) كما سنرى , من المهم بناء قاعدة القرار للتمييز بين المواقف حيث يكون <math>\sigma</math> معلوم و غير معلوم.
| |
| | |
|
| |
| '''<math>\sigma</math> معلوم:'''
| |
| | |
| | |
| لدينا <math>\sigma</math> معلوم, توزيع <math>\bar{X}</math> سيحدد بشكل كامل. لانستطيع عمل التكامل لتابع الكثافة الطبيعي للحصول على توابع التوزيع الطبيعية.
| |
| | |
| نعتمد على جداول الحلول الرقمية لأجل [[صورة:Mmengjavaimg2571.gif]].
| |
|
| |
|
| لذلك نعاير <math>\bar{X}</math> ونأخذ: | | لذلك نعاير <math>\bar{X}</math> ونأخذ: |
| سطر ١٦٣: |
سطر ١٥: |
|
| |
|
|
| |
|
| تطابق [[القيمة الحرجة]] لمستوى الدلالة <math>\alpha</math> والتي تأخذ من جدول التوزيع الطبيعي المعياري. | | تطابق <math> \mu _{0}</math> هو متوسط المجتمع الحقيقي. |
|
| |
| نكتب الأن مجالات القرار للأنواع الثلاثة للاختبار لأجل مستوى الدلالة <math>\alpha</math>. نعطي القيمة المتوقعة الحدية من <math>H_{0}</math> بمعنى: [[صورة:Mmengjavaimg2566.gif]] هو متوسط المجتمع الحقيقي.
| |
|
| |
|
|
| |
|
| سطر ١٧١: |
سطر ٢١: |
|
| |
|
|
| |
|
| يقع احتمال <math>V</math> في [[مجال الرفض]] للفرضية <math>H_{0}</math> والمساوية لمستوى الدلالة المعطاة <math>\alpha</math>: | | يقع احتمال <math>V</math> في <math> \mu _{0}</math>, يتضمن القيم الفعلية السالبة للاختبار الاحصائي <math>V</math>, انحرافات <math>V</math> عن <math>E(V) = 0</math> للجهة اليسرى للخط الحقيقي. |
| | |
| | |
| <math>P\left(V<c_{u}|\mu _{0}\right) +P\left( V>c_{o}|\mu _{0}\right) =\alpha /2+\alpha
| |
| /2=\alpha</math>
| |
| | |
| | |
| لأجل <math>P( V\leq c_{u})= 1 - \alpha/2</math> يمكن استعادة [[القيمة الحرجة]] العليا من جدول التوزيع الطبيعي المعياري <math>N(0; 1): c_{o} = z_{1 - \alpha/2}</math>
| |
| | |
| يتضمن تناظر المنحنى الطبيعي <math>c_{u} = -z_{1 - \alpha/2}</math>.
| |
| | |
| يعطى مجال الرفض لأجل <math>H_{0}</math> بواسطة:
| |
| | |
| | |
| | |
| <math>\left\{v|v<-z_{1-\alpha /2};\mbox{ }\;v>z_{1-\alpha /2}\right\}</math>.
| |
| | |
| | |
| | |
| ويعطى مجال القبول لأجل <math>H_{0}</math> :
| |
| | |
| | |
| | |
| <math>\left\{v|-z_{1-\alpha /2}\leq v\leq z_{1-\alpha /2}\right\}</math>
| |
| | |
| | |
| احتمال <math>V</math> يفترض القيمة من مجال القبول لأجل <math>H_{0}</math>
| |
| | |
| | |
| <math>P\left(c_{u}\leq V\leq c_{o}|\mu _{0}\right) =P\left(-z_{1-\alpha /2}\leq V\leq z_{1-\alpha /2}|\mu _{0}\right)=1-\alpha</math>
| |
| | |
| | |
| | |
| | |
| 2-الاختبار الأحادي الجانب الأيمن :
| |
| | |
| | |
| انحرافات [[الاختبار الاحصائي ]]المعياري <math>V</math> عن <math>E(V) = 0</math> للجهة اليمنى يميل لرفض <math>H_{0}</math>.
| |
| | |
| سيكون مجال الرفض مجموعة قيم الاختبار الاحصائي الموجب <math>v</math>, احتمال القيم الفعلية المشاهدة <math>V</math> ضمن هذا المجال مساوي لمستوى الدلالة المعطاة <math>\alpha</math>
| |
| | |
| | |
| <math>P\left(V>c|\mu _{0}\right) =\alpha</math>
| |
| | |
| | |
| لأجل: <math>P\left(V\leq c\right)=1-\alpha</math> نجد [[القيمة الحرجة]] في جدول تابع التوزيع الطبيعي المعياري التجميعي <math>N(0; 1):\; c=z_{1-\alpha }</math>
| |
| | |
| يعطى [[مجال الرفض]] لأجل <math>H_{0}</math> بواسطة:
| |
| | |
| | |
| | |
| <math>\left\{v|v>z_{1-\alpha}\right\}</math>
| |
| | |
| | |
| ويعطى مجال القبول لأجل <math>H_{0}</math> بواسطة:
| |
| | |
| | |
| | |
| <math>\left\{v|v\leq z_{1-\alpha }\right\}</math>.
| |
| | |
| | |
| | |
| احتمال <math>V</math> تفرض القيمة ضمن مجال القبول لأجل <math>H_{0}</math>:
| |
| | |
| | |
| | |
| <math>P\left( V\leq c|\mu _{0}\right)=P\left(V\leq z_{1-\alpha}|\mu _{0}\right)=1-\alpha</math>
| |
| | |
| | |
| | |
| 3-الاختبار الأحادي الجانب الأيسر:
| |
| | |
| | |
| | |
| متوسط العينات أصغر من [[صورة:Mmengjavaimg2566.gif]], يتضمن القيم الفعلية السالبة للاختبار الاحصائي <math>V</math>, انحرافات <math>V</math> عن <math>E(V) = 0</math> للجهة اليسرى للخط الحقيقي.
| |
|
| |
|
| في هذه الحالة يتألف مجال الرفض لأجل <math>H_{0}</math> من نتائج <math>V</math> السالبة | | في هذه الحالة يتألف مجال الرفض لأجل <math>H_{0}</math> من نتائج <math>V</math> السالبة |
| | | |
| لذلك [[القيمة الحرجة]] <math>c</math> ستكون سالبة. | | لذلك <math> \Prob\left( V<-c\vert\mu _{0}\right) =\alpha .</math> |
| | |
| مرة ثانية , يتضمن احتمال القيم الفعلية المشاهدة <math>V</math> ضمن مجال الرفض والمساوية الى <math>\alpha</math> :
| |
| | |
|
| |
|
|
| |
|
| [[صورة:Mmengjavaimg2590.gif]]
| | باستعمال خاصة التناظر للتوزيع الطبيعي, نستطيع ترجمة <math> \Prob\left( V<-c\right) </math> الى <math> 1-\Prob\left( V<c\right) </math> |
|
| |
|
| | لهذا القيمة المطلقة للقيمة الحرجة <math> \vert-c\vert=c</math> هي قيمة تابع التوزيع الطبيعي التجميعي للاحتمال <math>1-\alpha</math> |
|
| |
|
| باستعمال خاصة التناظر للتوزيع الطبيعي, نستطيع ترجمة [[صورة:Mmengjavaimg2591.gif]] الى [[صورة:Mmengjavaimg2592.gif]]
| | بمعنى:<math> c=z_{1-\alpha }</math> و <math> -c=-z_{1-\alpha }</math>. |
| | |
| لهذا القيمة المطلقة للقيمة الحرجة [[صورة:Mmengjavaimg2593.gif]] هي قيمة تابع التوزيع الطبيعي التجميعي للاحتمال <math>1-\alpha</math>
| |
| | |
| بمعنى:[[صورة:Mmengjavaimg2586.gif]] و [[صورة:Mmengjavaimg2594.gif]].
| |
|
| |
|
| يعطى مجال الرفض لأجل <math>H_{0}</math> بواسطة: | | يعطى مجال الرفض لأجل <math>H_{0}</math> بواسطة: |
| سطر ٣١٠: |
سطر ٨٠: |
| لأجل مستوى الدلالة المعطاة <math>\alpha</math> و<math>f=n-1</math> درجة الحرية, يمكن قراءة القيم الحرجة من جدول توزيع-t | | لأجل مستوى الدلالة المعطاة <math>\alpha</math> و<math>f=n-1</math> درجة الحرية, يمكن قراءة القيم الحرجة من جدول توزيع-t |
| | | |
| اذا أشرنا لتوزيع-t التجميعي مع درجة الحرية<math>f=n-1</math> لأجل الاحتمال <math>P</math> بواسطة: [[صورة:Mmengjavaimg2602.gif]] | | اذا أشرنا لتوزيع-t التجميعي مع درجة الحرية<math>f=n-1</math> لأجل الاحتمال <math>P</math> بواسطة: <math> t_{p;n-1}</math> |
|
| |
|
| نفرض [[صورة:Mmengjavaimg2566.gif]] متوسط المجتمع الحقيقي, لدينا مجالات القرار التالية لمواقف الاختبار: | | نفرض <math> \mu _{0}</math> متوسط المجتمع الحقيقي, لدينا مجالات القرار التالية لمواقف الاختبار: |
|
| |
|
|
| |
|
| سطر ٣١٨: |
سطر ٨٨: |
|
| |
|
|
| |
|
| [[مجا ل الرفض]] لأجل <math>H_{0}</math>:
| | <math> P\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{0}\right) =\alpha </math> |
| | |
| | |
| <math>\left\{v|v<-t_{1-\alpha/2;n-1}\mbox{ }v>t_{1-\alpha /2;n-1}\right\}</math>
| |
| | |
| | |
| | |
| مجال القبول لأجل <math>H_{0}</math>:
| |
| | |
| | |
| <math>\left\{ v|-t_{1-\alpha /2;n-1}\leq v\leq t_{1-\alpha /2;n-1}\right\}</math>
| |
| | |
| | |
| | |
| 2-الاختبار الأحادي الجانب الأيمن:
| |
| | |
| | |
| [[مجال الرفض]] لأجل <math>H_{0}</math>:
| |
| | |
| | |
| <math>\left\{v|v>t_{1-\alpha ;n-1}\right\}</math> | |
| | |
| | |
| مجال القبول لأجل <math>H_{0}</math>:
| |
| | |
| | |
| <math>\left\{v|v\leq t_{1-\alpha ;n-1}\right\}</math>
| |
| | |
| | |
| 3-الاختبار الأحادي الجانب الأيسر :
| |
| | |
| | |
| | |
| مجال الرفض لأجل <math>H_{0}</math>:
| |
| | |
| | |
| <math>\left\{v|v<t_{1-\alpha ;n-1}\right\}</math>
| |
| | |
| | |
| مجال القبول لأجل <math>H_{0}</math>:
| |
| | |
| | |
| <math>\left\{v|v\geq t_{1-\alpha ;n-1}\right\}</math>
| |
| | |
| | |
| ملاحظة: اذا حجم العينة كبير بشكل كافي <math> (n > 30)</math>, سيقرب توزيع-t بواسطة التوزيع الطبيعي المعياري.
| |
| | |
| ذلك يعني : <math>T</math>
| |
| يقرب للتوزيع <math>N(0; 1)</math>. يمكن قراءة القيم الحرجة من جداول التوزيع الطبيعي المعياري حينئذ لأجل <math>n</math>
| |
| كبيرة, نقدر <math>\sigma</math> بواسطة <math>S</math>
| |
| | |
| | |
| | |
| [[صورة:H100.gif]] ''' حساب الاختبار الاحصائي من العينة المشاهدة'''
| |
| | |
|
| |
| عندما حصلنا على [[العينة العشوائية]] <math>x_{1},\ldots ,x_{n}</math>, نحسب الخواص التجريبية لاختبارنا الاحصائي النظري المبنية على اجراءات اختبارنا.
| |
| | |
| على المستوى النظري
| |
| بيناهم في عبارات متغيرات العينة (النظرية) بمعنى: <math>X_{1},\ldots ,X_{n}</math> أي أشرنا لهم بالأحرف الكبيرة <math>V</math> , <math>\bar{X}</math> و <math>S</math>.
| |
| | |
| حسبت القيم الفعلية من العينة ذات الحجم <math>n</math>, <math>x_{1},\ldots ,x_{n}</math>
| |
| | |
| رمزت بواسطة <math>\bar{x}</math>, <math>v</math> و <math>s</math> حينئذ الصيغ التجريبية لمتوسط العينة والانحراف المعياري للعينة هي:
| |
| | |
| | |
| <math>\bar{x}=\frac{1}{n}\sum_{i=1}^{n}\; x_{i}</math>
| |
| | |
| | |
| و
| |
| | |
| | |
| <math>s =\sqrt{\frac{\sum_{i=1}^{n}\left( x_{i}-\bar{x}\right)^{2}}{n-1}}</math>
| |
| | |
| | |
| وفقا لذلك, قيمتا الاختبار الاحصائي الفعلتين لاختبار المتوسطات الطبيعية لأجل التباين المعلوم والمجهول هي:
| |
| | |
| | |
| <math>v=\frac{\bar{x}-\mu _{0}}{\sigma }\;\sqrt{n}</math>
| |
| | |
| | |
| و
| |
| | |
| | |
| <math>v=\frac{\overline{x}-\mu _{0}}{s}\sqrt{n}</math>
| |
| | |
| | |
| | |
| [[صورة:H100.gif]] ''' قرار الاختبار والتعاريف'''
| |
| | |
| | |
| اذا الاختبار الاحصائي <math>v</math> يقع في مجال الرفض , سترفض الفرضية الصفرية <math>H_{0}</math> على أساس العينة العشوائية من الحجم <math>n</math> ومستوى الدلالة <math>\alpha</math> المعطاة احصائيا.
| |
|
| |
| نقول بأن القيمة المتوقعة الحقيقية <math>E(X) = \mu</math> لا تساوي القيمة النظرية <math>\mu _{0}</math>
| |
| | |
| اذا العنصر الحقيقي لا ينتمي للمجال في الفرضية الصفرية <math>H_{0}</math> عملنا خطأ النوع الأول ("<math>H_{1}</math>"|<math>H_{0}</math>) .
| |
| | |
| في الواقع باختيار مستوى الدلالة المعين
| |
| قررنا حول احتمال عمل هذا الخطأ حيث تبنى مجالات القرار على احتمال عمل خطأ النوع الأول المساوي لمستوى الدلالة [[صورة:Mmengjavaimg2518.gif]]
| |
|
| |
|
| ومن جهة أخرى, <math>v</math> تقع في مجال القبول, تقودنا العينة المعطاة لقبول الفرضية الصفرية لأجل مستوى الدلالة المعطاة. | | ومن جهة أخرى, <math>v</math> تقع في مجال القبول, تقودنا العينة المعطاة لقبول الفرضية الصفرية لأجل مستوى الدلالة المعطاة. |
| سطر ٤٢٢: |
سطر ٩٤: |
| حينئذ غير قادرين أن نظهر احصائيا أن العنصر الصحيح <math>E(X) = \mu</math> ينحرف عن القيمة الصفرية <math>\mu _{0}</math> | | حينئذ غير قادرين أن نظهر احصائيا أن العنصر الصحيح <math>E(X) = \mu</math> ينحرف عن القيمة الصفرية <math>\mu _{0}</math> |
|
| |
|
| بذلك عملنا خطأ النوع الثاني بمعنى : [[الفرضية البديلة]] تصف الواقع بشكل صحيح:("<math>H_{0}</math>"|<math>H_{1}</math>). | | بذلك عملنا خطأ النوع الثاني بمعنى : <math> \Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \leq \... |
| | | ...ht) = \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{0}\right) \leq \alpha .</math> |
| كما أوضحناه احتمال عمل الخطأ <math>\Beta</math>. يكون بالعموم مجهول ومسبب لأجل قيم العنصر البديلة الفردية <math>\mu _{1}</math>
| |
| | |
| | |
| | |
| [[صورة:H100.gif]] '''القوة'''
| |
| | |
| | |
| كيف يمكن تقييم جودة الاختبار ؟ شاهدنا في اجراء الاختبار بأننا سيطرنا على احتمال عمل خطأ <math>\alpha</math> (بتعيين قيمة لمستوى الدلالة <math>\alpha</math>).
| |
| | |
| يحدد احتمال عمل الخطأ <math>\Beta</math> عندئذ بواسطة العنصر الصحيح (المجهول). صغر <math>\Beta</math> لأجل العنصر الحقيقي المعطى <math> \mu</math>.
| |
| | |
| بشكل أكيد سيرفض الاختبار بشكل متكرر أكثر الفرضية الصفرية عندما [[الفرضية البديلة]] صحيحة.
| |
| | |
| عندئذ لمستوى الدلالة المعطى المحدد , نريد <math>\Beta</math> لتكون أصغر ما يمكن لأجل مجالات العنصر الصحيح خارجا والمحددة في [[الفرضية الصفرية]] .
| |
| | |
| أو بشكل مكافئ نريد تعظيم احتمال عمل القرار الصحيح , ذلك يعني تعظيم المقدار <math>1-\Beta</math> لأي <math> \mu</math> صحيحة معطاة خارج مجال الفرضية الصفرية. بمعنى داخل مجال الفرضية البديلة.
| |
| | |
|
| |
| فكرة جودة الاختبار , تصور بما يدعى القوة , يحدد التابع احتمالات رفض <math>H_{0}</math> لقيم العنصر الصحيح <math> \mu</math> داخل مجال العنصر <math>H_{1}</math> لأجل <math>\alpha</math> المعطاة والعنصر النظري <math>\mu _{1}</math>
| |
| | |
| تقدم هذه الاحتمالات المتوسطات النظرية لعمل القرار الصحيح في رفض <math>H_{0}</math> لكل العينات الممكنة ( <math>\alpha</math> و <math> \mu</math> المعطاة). ويمكن حسابها بدون استعمال
| |
|
| |
|
| العينات الفعلية , في الواقع , تحسب القوة بسبب أننا نريد الحصول فقط على العينة المحددة وتهدف الى تحديد الدقة المتوقعة لاجراء الاختبار الفردي.
| |
|
| |
|
| تقنيا , تنتج القوة [[صورة:mmengjavaimg2616.gif]] احتمال رفض <math>H_{0}</math> للعناصر النظرية المعطاة <math>\mu</math>
| | اذا <math> =\Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \geq ... |
| | | ...}\right) \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{1}\right) =1-\beta .</math> |
| | |
| [[صورة:mmengjavaimg2617.gif]]
| |
| | |
| | |
| 1-الاختبار الثنائي الجانب:
| |
| | |
| | |
| في الاختبار الثنائي الجانب , [[الفرضية الصفرية]] صحيحة اذا وفقط اذا <math>\mu =\mu_{0}</math>.
| |
| | |
| رفض <math>H_{0}</math> يعني أننا عملنا الخطأ من النوع الأول:
| |
| | |
| | |
| | |
| [[صورة:mmengjavaimg2619.gif]]
| |
| | |
| | |
| | |
| لأجل كل قيم العنصر الممكنة, رفض <math>H_{0}</math> هو القرار الصحيح:
| |
| | |
| | |
| | |
| | |
| [[صورة:mmengjavaimg2620.gif]]
| |
| | |
| | |
| | |
| لدينا :
| |
| | |
| | |
| | |
| [[صورة:mmengjavaimg2621.gif]]
| |
| | |
| | |
| | |
| | |
| باستعمال الفرض الطبيعي حول التوزيع الاحتمالي , يمكننا حساب القوة لأجل حالة الاختبار الثنائي الجانب:
| |
| | |
| | |
| | |
| [[صورة:mmengjavaimg2622.gif]]
| |
| | |
| | |
| يمكن حساب احتمال خطأ النوع الثاني من القوة:
| |
| | |
| | |
| | |
| [[صورة:mmengjavaimg2623.gif]]
| |
| | |
| | |
| خواص القوة للاختبار الثنائي الجانب:
| |
| | |
| | |
| *لأجل <math>\mu = \mu_{0}</math> تفرض القوة الحد الأدنى <math>\alpha</math> .
| |
| | |
| *القوة متناظرة حول قيمة العنصر النظرية <math>\mu_{0}</math>.
| |
| | |
| *تزداد القوة مع زيادة بعد العنصر الحقيقي <math>\mu</math> عن النظري <math>\mu_{0}</math> وتقترب للواحد لما يزداد البعد الى [[صورة:mmengjavaimg1501.gif]] و [[صورة:mmengjavaimg30.gif]]على التوالي.
| |
| | |
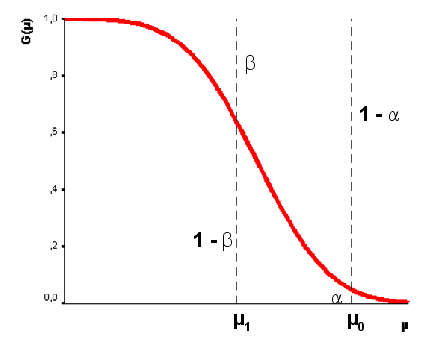
| تبين الخواص فقط منحنى القوة للشكل البياني التالي:
| |
| | |
| | |
| | |
| | |
| [[صورة:S2_51_14.gif]]
| |
| | |
| | |
| | |
| في الشكل البياني فوق , قيمتا العنصر الحقيقية البديلة <math>\mu_{1}</math> و <math>\mu_{2}</math> ,تبين اذا <math>\mu_{1}</math> العنصر الحقيقي, البعد <math>\mu_{1} - \mu_{0}</math> عالي نسبيا.
| |
| | |
| ولذلك احتمال <math>1 - \beta</math> عمل القرار الصحيح لقبول [[الفرضية البديلة]] <math>H_{1}</math> هو عالي نسبيا واحتمال عمل خطأ النوع الثاني <math>\beta</math> صغير.
| |
| | |
| بعد قيمة العنصر الحقيقية <math>\mu_{2}</math> عن قيمة العنصر النظرية <math>\mu</math> هو <math>\mu_{2} - \mu_{0}</math> صغير نسبيا.
| |
| | |
| عندئذ احتمال عمل القرار الصحيح لرفض [[الفرضية الصفرية ]], <math>1 - \beta</math> أصغر في المثال الأول , واحتمال عمل خطأ النوع الثاني <math>\beta</math> أكبر.
| |
| | |
| | |
| | |
| 2-الاختبار الأحادي الجانب الأيمن:
| |
| | |
| | |
| في الاختبار الأحادي الجانب الأيمن , [[الفرضية الصفرية]] صحيحة اذا العنصر الصحيح أقل من أو يساوي الى القيمة الحدية النظرية <math>\mu_{0}</math>, بمعنى اذا: <math>\mu \leq \mu_{0}</math>
| |
| | |
| وفي هذه الحالة الاحتمال الأكبر لرفض الفرضية الصفرية وعندئذ عمل خطأ النوع الأول مساوي لمستوى الدلالة <math>\alpha</math>
| |
| | |
| | |
| [[صورة:Mmengjavaimg2628.gif]]
| |
| | |
| | |
| اذا [[الفرضية البديلة]] بمعنى : <math>\mu>\mu_{0}</math> صحيحة نرفض الفرضية الصفرية وحينئذ
| |
| | |
| نعمل القرار الصحيح الذي يحدث مع الاحتمال:
| |
| | |
| | |
| | |
| [[صورة:Mmengjavaimg2630.gif]]
| |
|
| |
|
|
| |
|
| سطر ٥٥٢: |
سطر ١٠٧: |
|
| |
|
|
| |
|
| [[صورة:Mmengjavaimg2631.gif]]
| | <math> P\left( \mu \right)= \begin{cases}\Prob\left( \lq \text{H}_{1}^{\pri... |
| | ...me}\vert \text{H}_{1}\right)=1-\beta, & \text{if $ \mu > \mu_{0}.$} \end{cases}</math> |
|
| |
|
|
| |
|
| سطر ٥٦٠: |
سطر ١١٦: |
|
| |
|
|
| |
|
| [[صورة:Mmengjavaimg2632.gif]]
| | <math> P\left( \mu \right) =1-\Prob\left( V\leq z_{1-\alpha }-\frac{\mu -\mu _{0}}{ \sigma /\sqrt{n}}\right) .</math> |
|
| |
|
|
| |
|
| سطر ٥٦٨: |
سطر ١٢٤: |
|
| |
|
|
| |
|
| [[صورة:S2_51_17.gif]]
| | <math> \Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \geq \... |
| | | ...ht) = \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{0}\right) \leq \alpha .</math> |
| | |
| | |
| لأجل كل القيم داخل مجموعة العنصر للفرضية البديلة , تزداد القوة للواحد
| |
| كبر البعد <math>\mu -\mu_{0}</math>
| |
| | |
| ارتفاع الاحتمال <math>1 - \beta</math> لعمل القرار الصحيح لقبول [[الفرضية البديلة]]
| |
| | |
| وحينئذ صغر الاحتمال <math>\beta</math> لعمل خطأ النوع الثاني.
| |
| | |
| عند النقطة <math>\mu =\mu _{0}</math> القوة هي <math>\alpha</math> مستوى الدلالة المعطاة لأجل كل القيم الأخرى المتعلقة مع [[الفرضية الصفرية]] بمعنى: <math>\mu <\mu_{0}</math>, القوة أصغر من <math>\alpha</math>.
| |
| | |
| وهذا افترضناه عندما بنينا الاختبار
| |
| نريد <math>\alpha</math> لتكون الاحتمال الأكبر لرفض الفرضية الصفرية لأجل الفرضية الصفرية الصحيحة.
| |
| | |
| كما نرى من الشكل البياني ينقص هذا الاحتمال مع زيادة البعد المطلق <math>\mu -\mu_{0}</math>
| |
| | |
| | |
| | |
| 3-الاختبار الأحادي الجانب الأيسر:
| |
| | |
| | |
| في الاختبار الأحادي الجانب الأيسر , [[الفرضية الصفرية]] صحيحة اذا العنصر الحقيقي أكبر من أو يساوي للقيمة الحدية النظرية بمعنى اذا: <math>\mu \geq \mu _{0}</math>
| |
| | |
| في هذه الحالة رفض الفرضية الصفرية وعندئذ عمل خطأ النوع الأول , سيحدث مع الاحتمال الذي لا يتعدى <math>\alpha</math>
| |
| | |
| | |
| | |
| | |
| [[صورة:Mmengjavaimg2636.gif]]
| |
| | |
| | |
| | |
| اذا [[الفرضية البديلة]] صحيحة بمعنى: <math>\mu <\mu_{0}</math>
| |
| | |
| يعمل الباحث القرار الصحيح لرفض [[الفرضية الصفرية]]:
| |
|
| |
|
|
| |
|
|
| |
|
| [[صورة:Mmengjavaimg2637.gif]]
| | اذا <math> \Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \leq \... |
| | ...right) = \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{1}\right) =1-\beta .</math> |
|
| |
|
|
| |
|
| سطر ٦١٥: |
سطر ١٣٧: |
|
| |
|
|
| |
|
| [[صورة:Mmengjavaimg2638.gif]]
| | <math> P\left( \mu \right)= \begin{cases}\Prob\left( \lq \text{H}_{1}^{\pri... |
| | ...me}\vert \text{H}_{1}\right)=1-\beta, & \text{if $ \mu < \mu_{0}.$} \end{cases}</math> |
|
| |
|
|
| |
|
| سطر ٦٢٢: |
سطر ١٤٥: |
|
| |
|
|
| |
|
| [[صورة:Mmengjavaimg2639.gif]]
| | <math> P\left( \mu \right)=\Prob \left( V\leq -z_{1-\alpha} - \frac{\mu - \mu_{0}}{ \sigma / \sqrt{n}}\right).</math> |
|
| |
|
|
| |
|
.
لذلك نعاير 
ونأخذ:
لاختبارنا الاحصائي.
باعطاء 
صحيحة , 
له التوزيع الطبيعي المعياري (التقريبي):
تطابق 
هو متوسط المجتمع الحقيقي.
1-الاختبار الثنائي الجانب:
يقع احتمال في , يتضمن القيم الفعلية السالبة للاختبار الاحصائي , انحرافات عن 
للجهة اليسرى للخط الحقيقي.
في هذه الحالة يتألف مجال الرفض لأجل من نتائج السالبة
لذلك خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:17»): {\displaystyle \Prob\left( V<-c\vert\mu _{0}\right) =\alpha .}
باستعمال خاصة التناظر للتوزيع الطبيعي, نستطيع ترجمة خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:17»): {\displaystyle \Prob\left( V<-c\right) }
الى خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:19»): {\displaystyle 1-\Prob\left( V<c\right) }
لهذا القيمة المطلقة للقيمة الحرجة 
هي قيمة تابع التوزيع الطبيعي التجميعي للاحتمال 
بمعنى:
و 
.
يعطى مجال الرفض لأجل بواسطة:
ويعطى مجال القبول لأجل بواسطة:
احتمال يأخذ القيمة ضمن مجال القبول لأجل هو:
مجهول:
اذا ليست لدينا أي معرفة مسبقة حول الانحراف المعياري للمتغير العشوائي, نحتاج لنفكر بمقدر الاختبار الاحصائي:
يكون المقدر غير المتحيز لتباين المجتمع:
باستبدال بواسطة الجذر التربيعي الى 
نحصل على الاختبار الاحصائي الجديد:
اذا الفرضية الصفرية صحيحة , له توزيع-t (على الأقل تقريبي) مع درجة الحرية 
.
لأجل مستوى الدلالة المعطاة 
و درجة الحرية, يمكن قراءة القيم الحرجة من جدول توزيع-t
اذا أشرنا لتوزيع-t التجميعي مع درجة الحرية لأجل الاحتمال 
بواسطة: 
نفرض متوسط المجتمع الحقيقي, لدينا مجالات القرار التالية لمواقف الاختبار:
1-الاختبار الثنائي الجانب :
خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \lqin 1:25»): {\displaystyle P\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{0}\right) =\alpha }
ومن جهة أخرى, 
تقع في مجال القبول, تقودنا العينة المعطاة لقبول الفرضية الصفرية لأجل مستوى الدلالة المعطاة.
حينئذ غير قادرين أن نظهر احصائيا أن العنصر الصحيح 
ينحرف عن القيمة الصفرية 
بذلك عملنا خطأ النوع الثاني بمعنى : خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:17»): {\displaystyle \Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \leq \... ...ht) = \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{0}\right) \leq \alpha .}
اذا خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:18»): {\displaystyle =\Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \geq ... ...}\right) \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{1}\right) =1-\beta .}
تركيب هذه الصيغ للمجموعتين الثانويتين المنفصلتين لفضاء العنصر, يعطي القوة :
خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:51»): {\displaystyle P\left( \mu \right)= \begin{cases}\Prob\left( \lq \text{H}_{1}^{\pri... ...me}\vert \text{H}_{1}\right)=1-\beta, & \text{if $ \mu > \mu_{0}.$} \end{cases}}
نستطيع حساب القوة لمشكلة اختبارنا الأحادي الجانب الأيمن لأجل كل قيم العنصر الصحيحة الممكنة 
خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:40»): {\displaystyle P\left( \mu \right) =1-\Prob\left( V\leq z_{1-\alpha }-\frac{\mu -\mu _{0}}{ \sigma /\sqrt{n}}\right) .}
يعرض الشكل البياني التالي, الشكل المثالي للقوة لمشكلة الاختبار الأحادي الجانب الأيمن:
خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:17»): {\displaystyle \Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \geq \... ...ht) = \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{0}\right) \leq \alpha .}
اذا خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:17»): {\displaystyle \Prob\left( V\in \text{rejection region for H}_{0}\vert\mu \leq \... ...right) = \Prob\left( \lq \text{H}_{1}^{\prime }\vert\text{H}_{1}\right) =1-\beta .}
لكامل فضاء العنصر لدينا :
خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:51»): {\displaystyle P\left( \mu \right)= \begin{cases}\Prob\left( \lq \text{H}_{1}^{\pri... ...me}\vert \text{H}_{1}\right)=1-\beta, & \text{if $ \mu < \mu_{0}.$} \end{cases}}
لأجل المجتمع الموزع بشكل طبيعي ,نحسب احتمال رفض كتابع لقيمة العنصر الحقيقي
خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Illegal TeX function
Found \Probin 1:37»): {\displaystyle P\left( \mu \right)=\Prob \left( V\leq -z_{1-\alpha} - \frac{\mu - \mu_{0}}{ \sigma / \sqrt{n}}\right).}
يظهر الرسم الشكل البياني للقوة لأجل الاختبار الأحادي الجانب الأيسر
يعرف الشكل البياني بشكل مشابه كما في حالة الاختبار الأحادي الجانب الأيمن.
