Mengenlehre: Unterschied zwischen den Versionen
Aus MM*Stat
| Zeile 41: | Zeile 41: | ||
Das folgende [[Venn-Diagramm]] veranschaulicht dies: | Das folgende [[Venn-Diagramm]] veranschaulicht dies: | ||
[[Bild: | [[Bild:venn3.png]] | ||
====Vereinigung oder logische Summe von Ereignissen==== | ====Vereinigung oder logische Summe von Ereignissen==== | ||
Version vom 11. September 2018, 11:05 Uhr
Grundbegriffe
Element
Unter Elementen verstehen wir bestimmte wohlunterschiedene Objekte unserer Anschauung oder unseres Denkens. (Definition nach Georg Cantor)
Menge
Unter einer Menge verstehen wir jede Zusammenfassung von bestimmten wohlunterschiedenen Objekten unserer Anschauung oder unseres Denkens (welche die Elemente von genannt werden) zu einem Ganzen. (Definition nach Georg Cantor)
In der Wahrscheinlichkeitsrechnung werden Ereignisse als Teilmengen des Ereignisraumes definiert.
Da demnach Ereignisse Mengen sind, können die für Mengen definierten Relationen und Operationen (werden im Folgenden erklärt) direkt auf Ereignisse angewandt werden.
Klasse bzw. Gruppe
Die Vereinigung von Elementen nennt man Klasse bzw. Gruppe.
Beispiel: Die Menge sei gegeben durch . Eine Klasse der Menge wäre also z.B. .
Venn-Diagramm
Das Venn-Diagramm ist eine grafische Veranschaulichung von Ereignisraum und Ereignissen, die als Flächen abgebildet werden.
Relationen und Operationen von Ereignissen
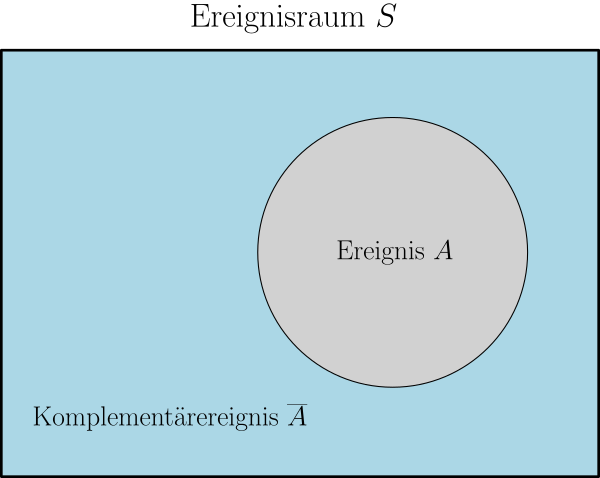
Leere Menge
Eine Menge , die kein Element enthält, heißt leere Menge. Man schreibt .
Bezogen auf ein Ereignis mit bedeutet dies, dass ein unmögliches Ereignis ist.
Teilmenge
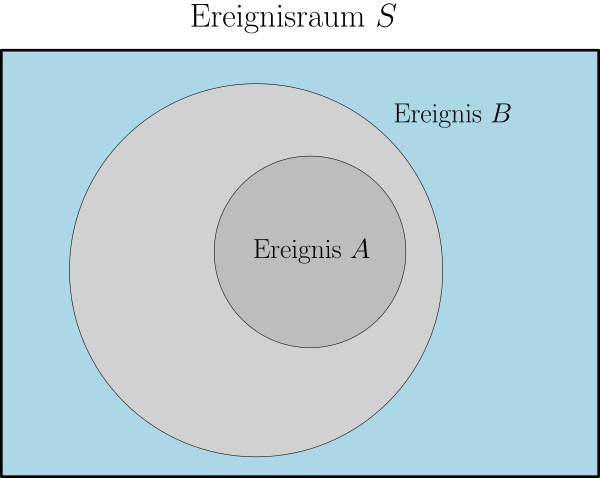
Eine Menge heißt Teilmenge einer Menge , wenn jedes Element von auch Element von ist. Teilmenge schreibt man als: .
Bezogen auf Ereignisse und mit bedeutet dies, dass wenn Ereignis eintritt, muss auch Ereignis eintreten.
Das folgende Venn-Diagramm veranschaulicht dies:
Vereinigung oder logische Summe von Ereignissen
Die Vereinigung oder logische Summe zweier Ereignisse und ist die Menge aller Elementarereignisse, die zu gehören. Man schreibt .
Die Vereinigung lässt sich über eine beliebige Anzahl von Ereignissen bilden:
| <R output="display">
pdf(rpdf,width=7, height=7) library("rJava") library("venneuler") library("graphics") venn.text <- function (vd, set="", xs=0, ys=0, ...) { x = y = 0
sets = strsplit(set, '&', fixed=T)
for (i in 1:length(sets)) {
if (length(setsi)==0) {
x <- min(vd$centers[,1]-vd$diameters/2)
y <- max(vd$centers[,2]+vd$diameters/2)
} else {
pos <- match(setsi, rownames(vd$centers))
x <- mean(vd$centers[pos,1])
y <- mean(vd$centers[pos,2])
}
text(x+xs, y+ys,cex=2.3, ...)
}
} venn <- function(...) { vd <- venneuler(unlist(list(...)))
vd$labels=c("","","")
par(mar=c(0.1,0.1,0.1,0.1), oma=c(0,0,3,0))
return(vd)
}
par(mfrow=c(2,1)) vd1 <- venn(A=25, B=25, "A&B"=10) vd1$colors <- c(0.3333333, 0.6666666, 1.0) vd2 <- venn(A=25, B=25, "A&B"=10) vd2$colors <- c(0.3333333, 0.3333333, 1.0) plot(vd1) text(0.18, 0.9, "Ereignisraum S", adj = c(0,0), cex=3.5) venn.text(vd1, "A", xs=0.12, ys=0.02, labels="Ereignis B") venn.text(vd1, "B", xs=-0.12, ys=0.02, labels="Ereignis A") box() title(main='Ereignisraum S', outer=TRUE, cex.main=2.5, font.main=1) plot(vd2) text(0.18, 0.9, "Ereignisraum S", adj = c(0,0), cex=3.5) venn.text(vd2, "A", xs=-0.05, ys=0.02, labels=expression(paste(A,union(B)))) venn.text(vd2, "B", xs=0.05, ys=0.02, labels="Ereignis") box() title(main='Ereignisraum S', outer=TRUE, cex.main=2.5, font.main=1) </R> |
Durchschnitt von Ereignissen
Der Durchschnitt zweier Ereignisse und ist die Menge aller Elementarereignisse, die sowohl zu als auch zu gehören. Man schreibt .
Die Verallgemeinerung der Durchschnittsoperation auf Ereignisse schreibt man als .
| <R output="display">
pdf(rpdf,width=7, height=7) library("rJava") library("venneuler") venn.text <- function (vd, set="", xs=0, ys=0, ...) { x = y = 0
sets = strsplit(set, '&', fixed=T)
for (i in 1:length(sets)) {
if (length(setsi)==0) {
x <- min(vd$centers[,1]-vd$diameters/2)
y <- max(vd$centers[,2]+vd$diameters/2)
} else {
pos <- match(setsi, rownames(vd$centers))
x <- mean(vd$centers[pos,1])
y <- mean(vd$centers[pos,2])
}
text(x+xs, y+ys,cex=2.7, ...)
}
} venn <- function(...) { vd <- venneuler(unlist(list(...)))
vd$labels=c("","","")
par(mar=c(0.1,0.1,0.1,0.1), oma=c(0,0,3.5,0))
return(vd)
} vd <- venn(A=25, B=25, "A&B"=10)
plot(vd)
venn.text(vd, "A", xs=0.11, ys=0.02, labels="Ereignis B") venn.text(vd, "B", xs=-0.11, ys=0.02, labels="Ereignis A") venn.text(vd, "A&B", xs=0.0, ys=-0.04, labels=expression(paste(A,intersect(B)))) box() title(main='Ereignisraum S', outer=TRUE, cex.main=3.5, font.main=1)
</R> |
Logische Differenz von Ereignissen
Das Ereignis ist die logische Differenz der Ereignisse und , wenn das Ereignis charakterisiert, bei dem aber nicht eintritt.
Man schreibt:
Disjunkte Ereignisse
Zwei Ereignisse und heißen disjunkt (sich ausschließend), wenn ihr gleichzeitiges Eintreten unmöglich ist und damit der Durchschnitt die leere Menge ist:
Wie aus den Beziehungen weiter oben ersichtlich, ist ein Ereignis stets zu seinem Komplementärereignis disjunkt.
Aber: Disjunkte Ereignisse sind nicht notwendig komplementär.
| <R output="display">
pdf(rpdf) library("rJava") library("venneuler") venn.text <- function (vd, set="", xs=0, ys=0, ...) { x = y = 0
sets = strsplit(set, '&', fixed=T)
for (i in 1:length(sets)) {
if (length(setsi)==0) {
x <- min(vd$centers[,1]-vd$diameters/2)
y <- max(vd$centers[,2]+vd$diameters/2)
} else {
pos <- match(setsi, rownames(vd$centers))
x <- mean(vd$centers[pos,1])
y <- mean(vd$centers[pos,2])
}
text(x+xs, y+ys,cex=3.5, ...)
}
} venn <- function(...) { vd <- venneuler(unlist(list(...)))
vd$labels=c("","","")
par(mar=c(0.1,0.1,0.1,0.1), oma=c(0,0,3.5,0))
return(vd)
} vd <- venn(A=0.4, B=0.4, "A&B"=-0.015)
plot(vd)
venn.text(vd, "A", xs=0.0, ys=0.0, labels="Ereignis B") venn.text(vd, "B", xs=0.0, ys=0.0, labels="Ereignis A") box() title(main='Ereignisraum S', outer=TRUE, cex.main=3.5, font.main=1)
|
Zerlegung des Ereignisraums
Ein System von Ereignissen heißt eine Zerlegung von , wenn
gilt und eines der Ereignisse bei einem Zufallsexperiment eintreten muss.
Eine Zerlegung kann man sich als eine Aufteilung aller Elementarereignisse in Gruppen vorstellen, wobei jedes Elementarereignis in genau einer Gruppe vorkommt (so wie man eine Schulklasse in Gruppen aufteilt).
Vollständige Zerlegung des Ereignisraums
Die Ereignisse bilden eine vollständige Zerlegung des Ereignisraumes , wenn
gilt.
Zusatzinformationen
Interpretation der Relationen und Operationen von Ereignissen
| Beschreibung des zugrundeliegenden
Sachverhaltes |
Bezeichnung
(Sprechweise) |
Darstellung |
| tritt sicher ein | ist sicheres Ereignis | |
| tritt sicher nicht ein | ist unmögliches Ereignis | |
| wenn eintritt, tritt ein | ist Teilmenge von | |
| genau dann, wenn eintritt, tritt ein | und sind äquivalente
Ereignisse |
|
| wenn eintritt, tritt nicht ein | und sind disjunkte Ereignisse | |
| genau dann, wenn eintritt, tritt nicht ein | und sind komplementäre Ereignisse | |
| genau dann, wenn mindestens eintritt (genau
dann, wenn oder oder eintreten), tritt ein |
ist Vereinigung der | |
| genau dann, wenn alle eintretten (genau dann,
wenn und und eintreten), tritt ein |
ist Durchschnitt der |
Beispiele
Vereinigung von Ereignissen
Zufallsexperiment: einmaliges Werfen eines Würfels
damit ergibt sich
Es gilt:
Durchschnitt von Ereignissen
Zufallsexperiment: einmaliges Werfen eines Würfels
damit ergibt sich
Es gilt:
Disjunkte vs. komplementäre Ereignisse
Zufallsexperiment: einmaliges Werfen eines Würfels
- ,
Aus den Ereignissen und ergibt sich:
damit ergibt sich
Die Ereignisse und sind komplementär und disjunkt
- ,
damit ergibt sich
Die Ereignisse und sind disjunkt, aber nicht komplementär (es gibt noch die Würfelzahlen 5 und 6)
Logische Differenz von Ereignissen
Zufallsexperiment: einmaliges Werfen eines Würfels
Dann sind:
und
Zerlegung des Ereignisraums
Zufallsexperiment: Werfen eines Würfels
.
Eine Zerlegung von ist mit den Ereignissen gegeben, denn es gilt:
.