Satz der totalen Wahrscheinlichkeit
Aus MM*Stat
Grundbegriffe
Satz der totalen Wahrscheinlichkeit
Sei eine Zerlegung von .
Dann gilt für ein beliebiges Ereignis mit unter Berücksichtigung des Multiplikationssatzes für beliebige Ereignisse:
Dabei wurde unter Verwendung des Multiplikationssatzes die Wahrscheinlichkeit durch ersetzt.
Beispiele
Wein
Der Genießer und Feinschmecker Wolfram S. hat natürlich einen Weinkeller. Darin lagert er seine Schätze.
Während er mit Eifer an dem Menü für heute Abend rührt, bei welchem er Hühnchen im Hauptgericht servieren wird, denkt er über seine Weißweinvorräte nach.
Wolfram S. weiß, dass er im besagten Keller Qualitätswein, Kabinett und Spätlese in einem Verhältnis von liegen hat.
Der Weißweinanteil bei diesen drei Sorten beträgt nach seiner Erfahrung bzw. .
Die Gäste, die sich heute bei Wolfram S. angesagt haben, sind keine besonderen Kenner.
Wolfram S. hat daher keine Lust, lange vor den Regalen zu stehen und zu überlegen, welchen Wein er anbieten soll.
Frage: Wie hoch ist die Wahrscheinlichkeit, beim ersten wahllosen Griff in die gefüllten Regale eine Weißweinflasche zu greifen?
Wolfram S. notiert zunächst die aus den Anteilen abgeleiteten Wahrscheinlichkeiten für die Weinsorten:
Dann stellt er fest, dass es sich bei dieser Unterteilung um eine vollständige Zerlegung des Ereignisraums handelt:
, .
Das heißt, außer seinen oben genannten drei Lieblingssorten lagert er keinen anderen Wein. Außerdem kann jede Flasche nur einer der drei Sorten zugeordnet werden.
Sei das Ereignis für Weißwein. Wolfram S. notiert die Wahrscheinlichkeit für Weißwein unter der Bedingung der drei Weinsorten:
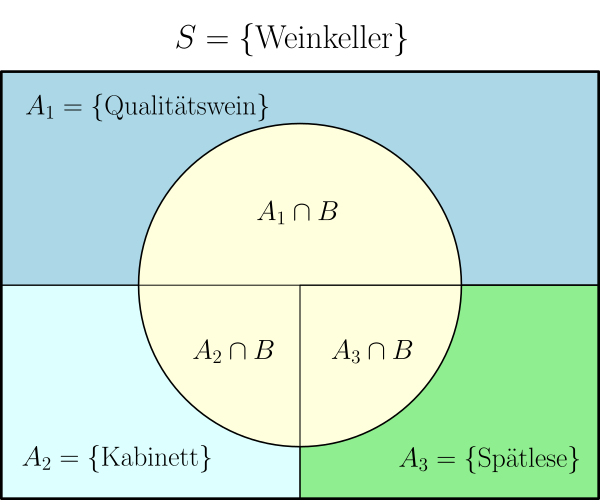
Um nicht die Übersicht zu verlieren, veranschaulicht sich der Feinschmecker das Problem an einem Venn-Diagramm:
Es fällt ihm leicht zu erkennen, dass er die Wahrscheinlichkeiten der Durchschnitte der Ereignisse von Weißwein mit jeder der drei Sorten addieren muss, um die Wahrscheinlichkeit für Weißwein zu erhalten.
Genau dies ist das Vorgehen nach dem Satz der totalen Wahrscheinlichkeit.
Da die drei Durchschnitte der Ereignisse disjunkt sind, kann er zur Berechnung von das Axiom 3 anwenden.
Formal schreibt sich das so:
Nun sind ihm aber die Wahrscheinlichkeiten der Durchschnitte der Ereignisse auf der rechten Seite nicht bekannt.
Da aber und , gegeben sind, ersetzt er die Wahrscheinlichkeiten nach dem Multiplikationssatz für beliebige Ereignisse und erhält:
Wolfram S. wird also beim einmaligen Hineingreifen in das Weinregal mit einer Wahrscheinlichkeit von eine Weißweinflasche erwischen.
Dieses Ergebnis heißt übrigens nicht, dass er spätestens beim vierten Mal blinden Zugreifens eine Weißweinflasche in der Hand hält.