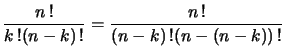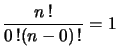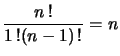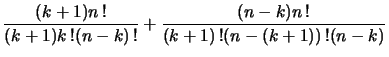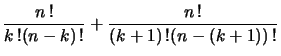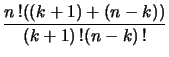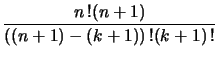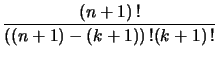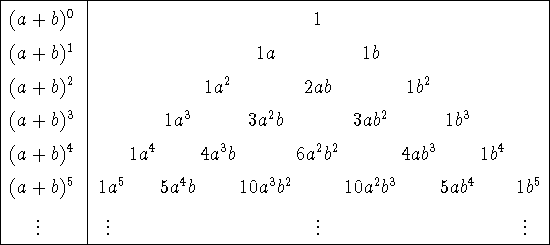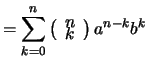الفرق بين المراجعتين لصفحة: «خواص أعداد اولر(الأعداد التوافقية )»

من MM*Stat Arabisch

اذهب إلى: تصفح, ابحث
لا ملخص تعديل
لا ملخص تعديل
 
سطر ١: سطر ١:
<math> \left(
[[صورة:H100.gif]] '''  4.5 خواص أعداد اولر(الأعداد التوافقية ) '''
\begin{array}{c}
n\\
k
\end{array} \right)</math>  في  النظرية التوافقية في أغلب الأحيان . لذا  من المفيد الحصول على الخواص  الهامة  المتعددة  لهذه الأعداد  التوافقية.




يستعمل  رمز اولر [[صورة:Mmengjavaimg794.gif]]  في  النظرية  التوافقية في أغلب الأحيان . لذا  من المفيد الحصول على الخواص  الهامة  المتعددة  لهذه  الأعداد  التوافقية.




<math> \left( \begin{array}{c} n\\ k \end{array} \right) = \left( \begin{array}{c} n\\ n-k \end{array} \right)</math>
 
 
[[صورة:H100.gif]]  '''      التناظر '''
 
 
 
[[صورة:Mmengjavaimg795.gif]]




سطر ١٦: سطر ١٩:




<math> \frac{n\,!}{k\,! (n-k)\,!} = \frac{n\,!}{(n-k)\,! (n-(n-k))\,!}</math>
[[صورة:Mmengjavaimg796.gif]]
 
 
 
 
[[صورة:H100.gif]]  '''الحالات  المحددة'''
 






[[صورة:Mmengjavaimg799.gif]] [[صورة:Mmengjavaimg798.gif]] [[صورة:Mmengjavaimg797.gif]]


<math> \frac{n\,!}{0\,! (n-0)\,!} = 1</math> <math> =</math> <math> \left( \begin{array}{c} n\\ 0 \end{array} \right)</math>




[[صورة:Mmengjavaimg801.gif]] [[صورة:Mmengjavaimg798.gif]] [[صورة:Mmengjavaimg800.gif]]


<math> \frac{n\,!}{1\,! (n-1)\,!} = n</math> <math> =</math> <math> \left( \begin{array}{c} n\\ 1 \end{array} \right)</math>




[[صورة:Mmengjavaimg803.gif]] [[صورة:Mmengjavaimg798.gif]] [[صورة:Mmengjavaimg802.gif]]


<math> \left( \begin{array}{c} n\\ n \end{array} \right) = 1</math> <math> =</math> <math> \left( \begin{array}{c} 0\\ 0 \end{array} \right)</math>




[[صورة:Mmengjavaimg806.gif]]  [[صورة:Mmengjavaimg805.gif]] [[صورة:Mmengjavaimg798.gif]] [[صورة:Mmengjavaimg804.gif]]


<math> \ k > n \geq 0</math>  <math> 0 \ </math> <math> =</math> <math> \left( \begin{array}{c} n\\ k \end{array} \right)</math>




[[صورة:H100.gif]]  '''    مجموع  عددي  اولر  '''


<math> \left( \begin{array}{c} n\\ k \end{array} \right) + \left( \begin...
 
...\end{array} \right) = \left( \begin{array}{c} n + 1\\ k + 1 \end{array} \right)</math>
 
[[صورة:Mmengjavaimg807.gif]]




سطر ٤٧: سطر ٥٨:




<math> \frac{(k+1)n\,!}{(k+1)k\,! (n-k)\,!} + \frac{(n-k)n\,!}{(k+1)\,! (n-(k+1))\,! (n-k)}</math> <math> =</math> <math> \frac{n\,!}{k\,! (n-k)\,!} + \frac{n\,!}{(k+1)\,! (n-(k+1))\,!}</math>
[[صورة:Mmengjavaimg809.gif]] [[صورة:Mmengjavaimg798.gif]] [[صورة:Mmengjavaimg808.gif]]
 
 
[[صورة:Mmengjavaimg810.gif]] [[صورة:Mmengjavaimg798.gif]]
 
 
[[صورة:Mmengjavaimg811.gif]] [[صورة:Mmengjavaimg798.gif]]
 
 
[[صورة:Mmengjavaimg812.gif]] [[صورة:Mmengjavaimg798.gif]]
 
 
[[صورة:Mmengjavaimg813.gif]] [[صورة:Mmengjavaimg798.gif]]
 
 
 
 
[[صورة:H100.gif]]  '''      أعداد اولر  والمعاملات  ذو الحدين '''
 
 
يحتوي الجدول التالي  في العمود  الأيسر  على العبارة الجبرية  ذات الشكل [[صورة:Mmengjavaimg814.gif]] وفي العمود الأيمن  التعابير  المأخوذة  بتوسيع  العبارات الجبرية  في العمود الأيسر .
 
 


[[صورة:Folnode6_e_8.gif]]


<math> \frac{n\,!((k+1) + (n-k))}{(k+1)\,! (n-k)\,!}</math> <math> =</math>


'''مثلث  باسكال''' 


<math> \frac{n\,! (n+1)}{((n+1) - (k+1))\,! (k+1)\,!}</math> <math> =</math>


في مثلث باسكال , توجد  كل المعاملات  من الجدول المقدم  فوق . نلاحظ  الارتباط الاضافي  بين سطري  المثلث .


<math> \frac{(n+1)\,!}{((n+1) - (k+1))\,! (k+1)\,!}</math> <math> =</math>




<math> \left( \begin{array}{c} n+1\\ k+1 \end{array} \right)</math> <math> =</math>






<TABLE CELLPADDING=3>
<TR><TD ALIGN="CENTER" COLSPAN=13>1</TD>
</TR>
<TR><TD ALIGN="CENTER" COLSPAN=5>&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER" COLSPAN=5>&nbsp;</TD>
</TR>
<TR><TD ALIGN="CENTER" COLSPAN=4>&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">2</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER" COLSPAN=4>&nbsp;</TD>
</TR>
<TR><TD ALIGN="CENTER" COLSPAN=3>&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">3</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">3</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER" COLSPAN=3>&nbsp;</TD>
</TR>
<TR><TD ALIGN="CENTER" COLSPAN=2>&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">4</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">6</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">4</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER" COLSPAN=2>&nbsp;</TD>
</TR>
<TR><TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">5</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">10</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">10</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">5</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
</TR>
<TR><TD ALIGN="CENTER">1</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">6</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">15</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">20</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">15</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">6</TD>
<TD ALIGN="CENTER">&nbsp;</TD>
<TD ALIGN="CENTER">1</TD>
</TR>
</TABLE>


<math> (a+b)^n</math> وفي العمود الأيمن  التعابير  المأخوذة  بتوسيع  العبارات الجبرية  في العمود الأيسر .






<math> (a+b)^6 = a^6 + 6a^5b + 15a^4b^2 + 20 a^3b^3 + 15a^2b^4 + 6ab^5 + b^6</math>
[[صورة:Mmengjavaimg815.gif]]




سطر ٨٠: سطر ١٧٩:




<math> (a+b)^n = \left( \begin{array}{c} n\\ 0 \end{array} \right) a^n +...
[[صورة:Mmengjavaimg816.gif]]
...ay} \right) ab^{n-1} +
\left( \begin{array}{c} n\\ n \end{array} \right) b^n = </math>






<math> = \sum_{k=0}^n \left( \begin{array}{c} n\\ k \end{array} \right) a^{n-k}b^k</math>
[[صورة:Mmengjavaimg817.gif]]

المراجعة الحالية بتاريخ ١٧:٤٩، ٣١ يوليو ٢٠٢٠

H100.gif 4.5 خواص أعداد اولر(الأعداد التوافقية )


يستعمل رمز اولر Mmengjavaimg794.gif في النظرية التوافقية في أغلب الأحيان . لذا من المفيد الحصول على الخواص الهامة المتعددة لهذه الأعداد التوافقية.



H100.gif التناظر


Mmengjavaimg795.gif


برهان التناظر


Mmengjavaimg796.gif



H100.gif الحالات المحددة



Mmengjavaimg799.gif Mmengjavaimg798.gif Mmengjavaimg797.gif


Mmengjavaimg801.gif Mmengjavaimg798.gif Mmengjavaimg800.gif


Mmengjavaimg803.gif Mmengjavaimg798.gif Mmengjavaimg802.gif


Mmengjavaimg806.gif Mmengjavaimg805.gif Mmengjavaimg798.gif Mmengjavaimg804.gif


H100.gif مجموع عددي اولر


Mmengjavaimg807.gif



اشتقاق الخاصة


Mmengjavaimg809.gif Mmengjavaimg798.gif Mmengjavaimg808.gif


Mmengjavaimg810.gif Mmengjavaimg798.gif


Mmengjavaimg811.gif Mmengjavaimg798.gif


Mmengjavaimg812.gif Mmengjavaimg798.gif


Mmengjavaimg813.gif Mmengjavaimg798.gif



H100.gif أعداد اولر والمعاملات ذو الحدين


يحتوي الجدول التالي في العمود الأيسر على العبارة الجبرية ذات الشكل Mmengjavaimg814.gif وفي العمود الأيمن التعابير المأخوذة بتوسيع العبارات الجبرية في العمود الأيسر .


Folnode6 e 8.gif


مثلث باسكال


في مثلث باسكال , توجد كل المعاملات من الجدول المقدم فوق . نلاحظ الارتباط الاضافي بين سطري المثلث .




1
  1   1  
  1   2   1  
  1   3   3   1  
  1   4   6   4   1  
  1   5   10   10   5   1  
1   6   15   20   15   6   1



Mmengjavaimg815.gif



نظرية ذي الحدين


تزود نظرية ذي الحدين الارتباط المذكور بين أعداد اولر و الأعداد التوافقية .


Mmengjavaimg816.gif


Mmengjavaimg817.gif

مجلوبة من «https://wikis.hu-berlin.de/mmara/w/index.php?title=خواص_أعداد_اولر(الأعداد_التوافقية_)&oldid=2472»