التوزيع الطبيعي

$\mu$ و $\sigma ,$ ويشار له $X\sim N(\mu ,\sigma ),$ اذا وفقط اذا تابع كثافته الاحتمالي  :

خطأ رياضيات (خطأ في التحويل. أبلغ الخادوم («cli») عن: «SyntaxError: Expected "-", "[", "\\", "\\begin", "\\begin{", "]", "^", "_", "{", "}", [ \t\n\r], [%$], [().], [,:;?!'], [/|], [0-9], [><~], [\-+*=], or [a-zA-Z] but "&" found.in 3:1»): {\displaystyle f_{N}V(x;\mu ,\sigma )= \frac{1}{\sigma \sqrt{2\pi }}e^{-(x-\mu )^{2}/2\sigma ^{2}}\quad -\infty &lt;x&lt;+\infty ,\sigma &gt;0 }

$F_{N}V(x;\mu ,\sigma )={\frac {1}{\sigma {\sqrt {2\pi }}}}\int \limits _{-\infty }^{x}e^{-(t-\mu )^{2}/2\sigma ^{2}}\,dt$

يعتمد التوزيع الطبيعي على العنصرين $\mu$ و $\sigma$ , أي $E(X)=\mu =\int \limits _{-\infty }^{+\infty }xf(x)\,dx,\quad V......{-\infty }^{+\infty }(x-\mu )^{2}f(x)\,dx,\quad \sigma ={\sqrt {{\sigma }^{2}}}$

خاصتان هامتان للمتغيرات العشوائية الطبيعية :

التحويل الخطي:

لدينا X موزع توزيع طبيعي $X\sim N(\mu ,\sigma )$ و Y هو تركيب خطي الى X: $Y=a+bX\,,b\neq 0$

عندئذ المتغير العشوائي Y له التوزيع الطبيعي أيضا :

$Y\sim N(a+b\mu ,\;|b|\cdot \sigma )$

قيم العناصر للمتغير العشوائي المحول , يتبع من قواعد الحساب مع القيم المتوقعة و التباينات:

$E(a+bX)=a+b\cdot E(X)$

$Var(a+bX)=b^{2}Var(X)=b^{2}{\sigma }^{2}$.

خاصة اعادة الانتاج  : دعنا نعتبر المتغيرات العشوائية n $X_{1},X_{2}\dots ,X_{n}$ مع التوزيعات الطبيعية $X_{i}\sim N(\mu _{i},\sigma _{i}),E(X_{i})=\mu _{i},Var(X_{i})=\sigma _{i}^{2}.$

مجموع المتغيرات العشوائية الموزعة طبيعيا والمستقلة $X_{1},\dots ,X_{n}$ , بمعنى

$Y=a_{1}X_{1}+a_{2}X_{2}+\dots +a_{n}X_{n},a_{i}\neq 0$

لأجل واحد على الأقل , ويكون له توزيع طبيعي ثانية

$Y=\sum \limits _{i=1}^{n}A_{i}X_{i}\sim N\left(\sum \limits _{i=1}^{n}a_{i}\mu _{i},{\sqrt {\sum \limits _{i=1}^{n}a_{i}^{2}\sigma _{i}^{2}}}\right)$

يعرض الشكل البياني تابع الكثافة والتوزيع للمتغير العشوائي ( N(2;1

تابع الكثافة الاحتمالي

$Z={\frac {X-\mu }{\sigma }}$

يشير المتغير العشوائي Z بالمتغير العشوائي المعياري الذي يتمركز حول متوسطه ويقاس بانحرافه المعياري.

اذا X موزع طبيعيا, عندئذ Z له التوزيع الطبيعي أيضا.

التوزيع الطبيعي المعياري :

يشار التوزيع Z عادة بالتوزيع الطبيعي المعياري (1 ; 0 ) N .

تابع الكثافة الاحتمالي للتوزيع الطبيعي المعياري:

$\varphi (z)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {z^{2}}{2}}}$

تابع التوزيع للتوزيع الطبيعي المعياري:

$\Phi (z)={\frac {1}{\sqrt {2\pi }}}\int \limits _{-\infty }^{z}e^{-v^{2}/2}\,dv$

القيمة المتوقعة و التباين للتوزيع الطبيعي المعياري :

Var(Z) = 1 E(Z) = 0

يعرض تابع الكثافة والتوزيع للمتغير العشوائي الطبيعي المعياري بالأشكال التالية:

تابع الكثافة الاحتمالي (N(0;1

$\mu ,\sigma$ )

$x=\mu +z\cdot \sigma ,z={\frac {x-\mu }{\sigma }}$

أي يشار:

$F_{NV}(x;\mu ,\sigma )=P(X\leq x)=P\left({\frac {X-\mu }{\sigma }}\leq {\frac {x-\mu }{\sigma }}\right)=P(Z\leq z)=\Phi (z)$

مجال الثقة:

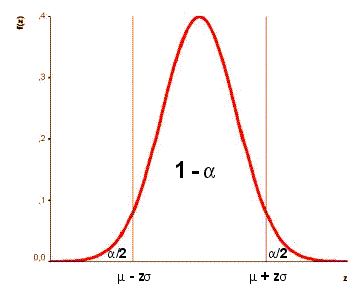
مجال الثقة للمتغير العشوائي X المجال مع الحدود $x_{l}$ و $x_{u}(x_{l}\leq x_{u})$

أي سيحتوي قيمة المتغير العشوائي X مع الاحتمال ( $\alpha$ - 1 ), بمعنى ($\alpha$ -1 .100% ) من كل قيم X التي ستقع في هذا المجال و ($\alpha$.100% ) ستقع خارج المجال ($\alpha$ - 1 ) يشار عادة كدرجة ثقة.

للقيم المعروفة من $\mu ,$ القيمة المتوقعة من X, يبنى المجال لجعل احتمال X يقع خارج هذه المنطقة ( توجد منطقتين) مع الاحتمال 2 / $\alpha$

ندعو المجال

($\mu -k\leq X\leq \mu +k$) = ($x_{u}\leq x_{o}$ )

مجال الثقة المتناظر مع درجة الثقة .

$\alpha$ - 1 =($x_{u}\leq X\leq x_{o}$ P )

لتأكيد على أهمية الانحراف المعياري كعنصر قياس , انحراف X عن قيمته المتوقعة $\mu$ يقاس عادة بالجداء من $\sigma$

مجال الثقة له الصيغة

X $\sigma \leq$ c - $\mu$

اذا المتغير العشوائي X هو N( $\mu ,\sigma$ ) عندئذ لأجل $\sigma$ c + $\mu$ x=

الصيغ التالية:

${\frac {x-\mu }{\sigma }}={\frac {\mu +c\sigma -mu}{\sigma }}$

$z=c$

و P(Z $\leq$ z ) = $\Phi$ (z) = 1 - $\alpha$ /2 .

القيمة الحرجة $z_{1-\alpha /2}$ للاحتمال $\alpha$/2 - 1 يتم الحصول عليه من قيم الجدول للتوزيع الطبيعي المعياري .

باستعمال هذه القيم نحصل على مجال الثقة للمتغير العشوائي الموزع طبيعيا:

$[\mu -z_{1-\alpha /2}\sigma \leq X\leq \mu +z_{1-\alpha /2}\sigma ]$

والاحتمال "لهذا المجال":

$P(\mu -z_{1-\alpha /2}\sigma \leq X\leq \mu +z_{1-\alpha /2}\sigma )=1-\alpha$

مجال الثقة للمتغير العشوائي الموزع طبيعيا:

أي:

$P(\mu -z_{1-\alpha /2}\sigma \leq X\leq \mu +z_{1-\alpha /2}\sigma )=2\Phi (z)-1$.

لأجل z المعطاة نحسب درجات الثقة للمجال:

$P(\mu -z_{1-\alpha /2}\sigma \leq X\leq \mu +z_{1-\alpha /2}\sigma )$
	$0,6827\quad {\mbox{for }}\quad z=1$
	$0,9545\quad {\mbox{for }}\quad z=2$
	$0,9973\quad {\mbox{for}}\quad z=3$

من جهة أخرى نجد أيضا القيمة z التي تنتج درجة الثقة المطلوبة $\alpha$ - 1

مثال:

$P(\mu -z_{1-\alpha /2}\sigma \leq X\leq \mu +z_{1-\alpha /2}\sigma )=0,95</mathz=1,96$