Univariate Statistik/Aufgaben: Unterschied zwischen den Versionen
Aus MM*Stat
Keine Bearbeitungszusammenfassung |
|||
| (44 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie:Aufgaben]] | |||
{{Loesung|Anstieg der Produktion|0}} | |||
Im Unternehmen U stieg die Produktion des Erzeugnisses E von 2005 bis 2007 im Mittel jährlich um 10%, von 2007 bis 2009 im Mittel jährlich um 20%. | Im Unternehmen U stieg die Produktion des Erzeugnisses E von 2005 bis 2007 im Mittel jährlich um 10%, von 2007 bis 2009 im Mittel jährlich um 20%. | ||
| Zeile 10: | Zeile 8: | ||
* Auf wieviel Prozent würde die E–Produktion 2011 gegenüber 2007 bei Fortsetzung des mittleren Entwicklungstempos von 2007 bis 2009 steigen? | * Auf wieviel Prozent würde die E–Produktion 2011 gegenüber 2007 bei Fortsetzung des mittleren Entwicklungstempos von 2007 bis 2009 steigen? | ||
{{Loesung|Arbeitslose|1}} | |||
Ein Bundesland ist in zwei Arbeitsamtsbezirke eingeteilt. In diesen werden für einen bestimmten Monat folgende Anteile der Arbeitslosen an den Erwerbspersonen (Arbeitslosenquote) und Arbeitslosenzahlen ermittelt: | Ein Bundesland ist in zwei Arbeitsamtsbezirke eingeteilt. In diesen werden für einen bestimmten Monat folgende Anteile der Arbeitslosen an den Erwerbspersonen (Arbeitslosenquote) und Arbeitslosenzahlen ermittelt: | ||
| Zeile 30: | Zeile 29: | ||
Bestimmen sie die Arbeitslosenquote für dieses Bundesland. | Bestimmen sie die Arbeitslosenquote für dieses Bundesland. | ||
{{Loesung|Auswirkung der Regelstudienzeit|2}} | |||
Um die Auswirkung der Regelstudienzeit zu demonstrieren, wurden im Januar die Studienzeiten von 200 Wirtschaftsingenieuren in der Bundesrepublik Deutschland erhoben, die in den vergangenen 4 Semestern ihr Studium abgeschlossen haben. Es ergaben sich folgende Daten (fiktive Daten): | Um die Auswirkung der Regelstudienzeit zu demonstrieren, wurden im Januar die Studienzeiten von 200 Wirtschaftsingenieuren in der Bundesrepublik Deutschland erhoben, die in den vergangenen 4 Semestern ihr Studium abgeschlossen haben. Es ergaben sich folgende Daten (fiktive Daten): | ||
| Zeile 93: | Zeile 71: | ||
* Ist es sinnvoll, bei einem nominalskalierten Merkmal eine Verteilungsfunktion anzugeben? Begründen Sie Ihre Antwort. | * Ist es sinnvoll, bei einem nominalskalierten Merkmal eine Verteilungsfunktion anzugeben? Begründen Sie Ihre Antwort. | ||
{{Loesung|Benzinverbrauch|3}} | |||
Bei einer Testreihe, die den Benzinverbrauch eines Autotyps in Deutschland erfasste, erhielt man folgende Daten: | Bei einer Testreihe, die den Benzinverbrauch eines Autotyps in Deutschland erfasste, erhielt man folgende Daten: | ||
| Zeile 102: | Zeile 81: | ||
Für den Export in die USA müssen die Verbrauchsdaten in Gallonen/100 Meilen angegeben werden (1 Gallone = 3,785 Liter, 1 Meile = 1,609km) Welchen Wert hat der Variationskoeffizient v, wenn der Benzinverbrauch in Gallonen/100 Meilen ausgewiesen wird? | Für den Export in die USA müssen die Verbrauchsdaten in Gallonen/100 Meilen angegeben werden (1 Gallone = 3,785 Liter, 1 Meile = 1,609km) Welchen Wert hat der Variationskoeffizient v, wenn der Benzinverbrauch in Gallonen/100 Meilen ausgewiesen wird? | ||
{{Loesung|Berliner Luftqualität|4}} | |||
An einer Messstation zur Kontrolle des Stickstoffmonoxydgehalts in der Berliner Luft wurden im März an 15 Tagen die folgenden Werte ermittelt (<math>mg/m^3</math>): | An einer Messstation zur Kontrolle des Stickstoffmonoxydgehalts in der Berliner Luft wurden im März an 15 Tagen die folgenden Werte ermittelt (<math>mg/m^3</math>): | ||
| Zeile 141: | Zeile 113: | ||
* Wieviel Stickstoffmonoxydgehalt war an den 80% “saubersten” Tagen höchstens in der Luft? | * Wieviel Stickstoffmonoxydgehalt war an den 80% “saubersten” Tagen höchstens in der Luft? | ||
{{Loesung|Besuche pro Woche|5}} | |||
50 Studenten wurden danach gefragt, wie oft sie in der vergangenen Woche ihre Freundin besucht haben. Das Ergebnis ist folgendes: | 50 Studenten wurden danach gefragt, wie oft sie in der vergangenen Woche ihre Freundin besucht haben. Das Ergebnis ist folgendes: | ||
| Zeile 222: | Zeile 178: | ||
* Wie oft besuchte ein Student durchschnittlich seine Freundin? | * Wie oft besuchte ein Student durchschnittlich seine Freundin? | ||
{{Loesung|Bevölkerungsdichte und Ärztedichte|6}} | |||
Für die drei Regionen eines Landes sind jeweils die Bevölkerungsdichte X (Einwohner je km<math>^2</math>) und die Ärztedichte Y (Ärzte je 1 000 Einwohner) gegeben: | Für die drei Regionen eines Landes sind jeweils die Bevölkerungsdichte X (Einwohner je km<math>^2</math>) und die Ärztedichte Y (Ärzte je 1 000 Einwohner) gegeben: | ||
| Zeile 262: | Zeile 219: | ||
Berechnen Sie die Bevölkerungsdichte X und die Ärztedichte Y für das gesamte Land. | Berechnen Sie die Bevölkerungsdichte X und die Ärztedichte Y für das gesamte Land. | ||
{{Loesung|Bibliotheken - Teil I|7}} | |||
Aus der Erhebung “Deutsche Bibliotheksstatistik ”, Berlin , wurden für die zentralen Universitätsbibliotheken nachstehende Angaben über die Öffnungszeiten (Std./Wo.), die Ausleihzeiten (Std./Wo), den Etat für Neuerwerb (Mrd. EUR/Jahr) und die Planstellen entnommen: | Aus der Erhebung “Deutsche Bibliotheksstatistik ”, Berlin , wurden für die zentralen Universitätsbibliotheken nachstehende Angaben über die Öffnungszeiten (Std./Wo.), die Ausleihzeiten (Std./Wo), den Etat für Neuerwerb (Mrd. EUR/Jahr) und die Planstellen entnommen: | ||
| Zeile 682: | Zeile 625: | ||
</li></ul> | </li></ul> | ||
{{Loesung|Bibliotheken - Teil II|8}} | |||
Das Bruttoeinkommen aus unselbständiger Arbeit je Beschäftigten und Monat in der Bundesrepublik Deutschland stieg von 3 012 DM im Jahre 1980 auf 4 112 DM im Jahre 1989. Die Nettolohn– und –gehaltssumme je Beschäftigten und Monat veränderte sich von 1 765 DM im Jahre 1980 auf 2 261 DM im Jahre 1989.<br /> | Die folgenden Fragen beziehen sich auf die Häufigkeitsverteilungen der klassierten Daten der [Aufgabe12]. | ||
* Berechnen Sie drei aussagekräftige Mittelwerte für das Erhebungsmerkmal <math>X</math>: “Öffnungszeiten”. | |||
* Ermitteln Sie ebenfalls drei sinnvolle Mittelwerte für das Erhebungsmerkmal <math>Y</math>: “Ausleihzeiten”. | |||
* Ist der Modus ein aussagekräftiger Mittelwert für das Erhebungsmerkmal <math>Z</math>: “Etat für Neuerwerb”? | |||
* Berechnen Sie für das Merkmal <math>Z</math>: “Etat für Neuerwerb” die Quartile. Zeichnen Sie einen Boxplot. | |||
{{Loesung|Bibliotheken - Teil III|9}} | |||
In [Aufgabe12] wurden für die zentralen Universitätsbibliotheken der Bundesrepublik Deutschland unter anderem die beiden Merkmale <math>X</math>: “Öffnungszeiten” und <math>Y</math>: “Ausleihzeiten” untersucht. Beantworten Sie ausgehend von den Häufigkeitsverteilungen der klassierten Daten der Merkmale folgende Frage: | |||
Welches der beiden Merkmale weist die größere Streuung auf Basis der Standardabweichung auf? (Runden Sie für Ihre Berechnungen den zugrundegelegten Mittelwert auf eine Stelle nach dem Komma.) | |||
{{Loesung|Brutto- und Nettoeinkommen|10}} | |||
Das Bruttoeinkommen aus unselbständiger Arbeit je Beschäftigten und Monat in der Bundesrepublik Deutschland stieg von 3 012 DM im Jahre 1980 auf 4 112 DM im Jahre 1989. Die Nettolohn– und –gehaltssumme je Beschäftigten und Monat veränderte sich von 1 765 DM im Jahre 1980 auf 2 261 DM im Jahre 1989.<br /> | |||
<span>Quelle: Zahlen zur wirtschaftlichen Entwicklung der Bundesrepublik<br /> | <span>Quelle: Zahlen zur wirtschaftlichen Entwicklung der Bundesrepublik<br /> | ||
Deutschland 1991, Institut der Deutschen Wirtschaft Köln, S. 30.</span> | Deutschland 1991, Institut der Deutschen Wirtschaft Köln, S. 30.</span> | ||
| Zeile 690: | Zeile 651: | ||
Vergleichen Sie das Bruttoeinkommen und das Nettoeinkommen je Beschäftigten bezüglich ihres mittleren Entwicklungstempo im Zeitraum 1980–1989. | Vergleichen Sie das Bruttoeinkommen und das Nettoeinkommen je Beschäftigten bezüglich ihres mittleren Entwicklungstempo im Zeitraum 1980–1989. | ||
{{Loesung|CDs|11}} | |||
In der Umsatzstatistik eines Einzelhändlers für das zurückliegende Geschäftsjahr sind für die drei Sorten CDs folgende Preise und Umsätze ausgewiesen: | |||
{|class="wikitable" | {|class="wikitable" | ||
! Sorte | |||
!align="right"| 1 | |||
!align="right"| 2 | |||
!align="right"| 3 | |||
|- | |- | ||
|align="right"| | | Preis | ||
|align="right"| 3,90 | |||
|align="right"| | |align="right"| 4,50 | ||
|align="right"| | |align="right"| 4,90 | ||
|- | |- | ||
| | | Umsatz | ||
|align="right"| 1224,60 | |||
|align="right"| 967,50 | |||
|align="right"| 519,40 | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|} | |} | ||
* Berechnen Sie den Durchschnittspreis für CDs im vergangenen Geschäftsjahr. | |||
* Berechnen Sie die Standardabweichung des Preises für CDs. | |||
{{Loesung|Das erste Tor|12}} | |||
Der folgenden Liste ist zu entnehmen, wieviele Minuten man bei jedem von 25 Fußballspielen warten musste, bis das erste Tor fiel: | |||
{|class="wikitable" | |||
{|class="wikitable" | |||
|align="right"| 40; | |align="right"| 40; | ||
|align="right"| 65; | |align="right"| 65; | ||
| Zeile 817: | Zeile 723: | ||
Auf der Grundlage einer Gruppierung mit vier Klassen (1. Klasse: 0 - 15, 2. Klasse: 15 - 30, 3. Klasse: 30 - 45, 4. Klasse: 45 - 90min) beantworten Sie die Frage zu: Wie groß ist der Anteil der Spiele, bei denen man mehr als 20, aber höchstens 60 Minuten auf das erste Tor warten musste? | Auf der Grundlage einer Gruppierung mit vier Klassen (1. Klasse: 0 - 15, 2. Klasse: 15 - 30, 3. Klasse: 30 - 45, 4. Klasse: 45 - 90min) beantworten Sie die Frage zu: Wie groß ist der Anteil der Spiele, bei denen man mehr als 20, aber höchstens 60 Minuten auf das erste Tor warten musste? | ||
{{Loesung|Ladekabel|13}} | |||
In den Städten A, B und C wurden jeweils in mehreren Geschäften die Preise für einen bestimmtes Ladekabel ermittelt. Im Ort A ergab sich aufgrund von 11 Einzelwerten ein Durchschnittspreis von 16,44 EUR. In B betrug der Durchschnittspreis basierend auf 6 Einzelwerten 15,28 EUR und in C wurde nach dem Besuch von 13 Geschäften als Durchschnittspreis 14,86 EUR ermittelt. | In den Städten A, B und C wurden jeweils in mehreren Geschäften die Preise für einen bestimmtes Ladekabel ermittelt. Im Ort A ergab sich aufgrund von 11 Einzelwerten ein Durchschnittspreis von 16,44 EUR. In B betrug der Durchschnittspreis basierend auf 6 Einzelwerten 15,28 EUR und in C wurde nach dem Besuch von 13 Geschäften als Durchschnittspreis 14,86 EUR ermittelt. | ||
| Zeile 823: | Zeile 730: | ||
Wie hoch ist der Durchschnittspreis des Ladekabels unter Berücksichtigung sämtlicher Preisinformationen aus den Städten A, B und C? | Wie hoch ist der Durchschnittspreis des Ladekabels unter Berücksichtigung sämtlicher Preisinformationen aus den Städten A, B und C? | ||
{{Loesung|Drei Betriebe|14}} | |||
Für die 3 Betriebe eines Unternehmens liegen folgende Angaben vor (TEUR = 1000 EUR): | Für die 3 Betriebe eines Unternehmens liegen folgende Angaben vor (TEUR = 1000 EUR): | ||
| Zeile 871: | Zeile 775: | ||
* Wie hoch wird voraussichtlich der Materialverbrauch des Unternehmens im Jahre 2013 sein, wenn das mittlere jährliche Entwicklungstempo des Zeitraumes 2007 – 2011 weiterhin beibehalten wird? | * Wie hoch wird voraussichtlich der Materialverbrauch des Unternehmens im Jahre 2013 sein, wenn das mittlere jährliche Entwicklungstempo des Zeitraumes 2007 – 2011 weiterhin beibehalten wird? | ||
{{Loesung|Drei Stichproben|15}} | |||
Von drei verschiedenen Stichproben mit nur positiven Beobachtungswerten sind folgende Informationen gegeben: | Von drei verschiedenen Stichproben mit nur positiven Beobachtungswerten sind folgende Informationen gegeben: | ||
| Zeile 899: | Zeile 804: | ||
Die drei Stichproben werden zu einer einzigen Stichprobe vereinigt. Berechnen Sie die Varianz für die gesamte Stichprobe. | Die drei Stichproben werden zu einer einzigen Stichprobe vereinigt. Berechnen Sie die Varianz für die gesamte Stichprobe. | ||
{{Loesung|Eine Befragung von Studierenden - Teil I|16}} | |||
Für eine Untersuchung von Studierenden an einer deutschen Hochschule wurden im Juni 25 Studierende nach dem Studiengang, der Anzahl der Geschwister und nach dem Einkommen befragt. Das Ergebnis war: | |||
Für eine Untersuchung von Studierenden an einer deutschen Hochschule wurden im Juni 25 Studierende nach dem Studiengang, der Anzahl der Geschwister und nach dem Einkommen befragt. Das Ergebnis war: | |||
{|class="wikitable" | {|class="wikitable" | ||
| Zeile 1.092: | Zeile 988: | ||
** Welches Einkommen hatten die 20% einkommensstärksten Studierenden mindestens? | ** Welches Einkommen hatten die 20% einkommensstärksten Studierenden mindestens? | ||
{{Loesung|Eine Befragung von Studierenden - Teil II|17}} | |||
Bezogen auf die Aufgabe [[Univariate Statistik/Aufgaben#Eine Befragung von Studierenden - Teil I|davor]]. | |||
* Ermitteln Sie einen geeigneten Lageparameter für das Erhebungsmerkmal <math>X</math>: “Studiengang”. | |||
* Ermitteln Sie drei geeignete Lageparameter für das Erhebungsmerkmal <math>Y</math>: “Anzahl der Geschwister”. | |||
* Berechnen Sie basierend auf der Urliste das durchschnittliche Einkommen eines/einer Studierenden. | |||
* Berechnen Sie basierend auf der Häufigkeitsverteilung der klassierten Daten des Erhebungsmerkmals <math>Z</math>: “Einkommen” zwei aussagekräftige Lageparameter, die Quartile und das 90%–Quantil. | |||
* Geben Sie für das Merkmal “Einkommen” die 5 - Zahlen - Zusammenfassung (Min, Max, Median, unteres und oberes Quartil) an und zeichnen Sie den Box–Plot. | |||
{{Loesung|Einkommen der Beamten|18}} | |||
In der Auswertung einer statistischen Erhebung vom April 2012 erhielt die Hälfte der befragten Beamten in einer Region ein monatliches Nettoeinkommen unter 2590 EUR. 1/4 der Beamten erhielten mehr als 3590 EUR. Während die gesamte Einkommensspannweite mit 8000 EUR angegeben wird, wird für die mittleren 50% der Beamten eine Einkommensspannweite von 1770 EUR ausgewiesen. Das geringste Einkommen lag bei 500 EUR. Die Standardabweichung der Nettoeinkommen wird mit 1620 EUR angegeben. Das sind 54% des durchschnittlichen Nettoeinkommens.<br /> | In der Auswertung einer statistischen Erhebung vom April 2012 erhielt die Hälfte der befragten Beamten in einer Region ein monatliches Nettoeinkommen unter 2590 EUR. 1/4 der Beamten erhielten mehr als 3590 EUR. Während die gesamte Einkommensspannweite mit 8000 EUR angegeben wird, wird für die mittleren 50% der Beamten eine Einkommensspannweite von 1770 EUR ausgewiesen. Das geringste Einkommen lag bei 500 EUR. Die Standardabweichung der Nettoeinkommen wird mit 1620 EUR angegeben. Das sind 54% des durchschnittlichen Nettoeinkommens.<br /> | ||
Bestimmen Sie das 25%–Quartil des Nettoeinkommens der befragten Beamten. | Bestimmen Sie das 25%–Quartil des Nettoeinkommens der befragten Beamten. | ||
{{Loesung|Einkommensgleichheit|19}} | |||
Ein Ökonom möchte die relative Einkommensgleichheit auf den drei melanesischen Inseln Atoll A, B und C vergleichen. Auf jeder Insel leben 8 Personen. Zahlungsmittel auf den Inseln sind Kauri Schnecken. Als geeignetes Maß erscheint dem Ökonomen der Variationskoeffizient. Berechnen Sie diesen für Atoll A mit folgender Einkommenstabelle. | Ein Ökonom möchte die relative Einkommensgleichheit auf den drei melanesischen Inseln Atoll A, B und C vergleichen. Auf jeder Insel leben 8 Personen. Zahlungsmittel auf den Inseln sind Kauri Schnecken. Als geeignetes Maß erscheint dem Ökonomen der Variationskoeffizient. Berechnen Sie diesen für Atoll A mit folgender Einkommenstabelle. | ||
| Zeile 1.134: | Zeile 1.043: | ||
|} | |} | ||
{{Loesung|Einkommen und Alter|20}} | |||
50 Personen wurden nach dem Einkommen (EUR) und dem Alter (Jahre) befragt. Im Ergebnis ergab sich nachstehende Korrelationstabelle: | 50 Personen wurden nach dem Einkommen (EUR) und dem Alter (Jahre) befragt. Im Ergebnis ergab sich nachstehende Korrelationstabelle: | ||
| Zeile 1.200: | Zeile 1.110: | ||
* Berechnen Sie die Kovarianz zwischen Einkommen und Alter. | * Berechnen Sie die Kovarianz zwischen Einkommen und Alter. | ||
{{Loesung|Einwohnerzahlen|21}} | |||
Für das Jahr 1980 wurden nachstehende Einwohnerzahlen (in Millionen) im Fischer–Weltalmanach 2000 veröffentlicht. | Für das Jahr 1980 wurden nachstehende Einwohnerzahlen (in Millionen) im Fischer–Weltalmanach 2000 veröffentlicht. | ||
| Zeile 1.245: | Zeile 1.156: | ||
Berechnen Sie einen aussagekräftigen Mittelwert. | Berechnen Sie einen aussagekräftigen Mittelwert. | ||
{{Loesung|Eiskugelkonsum|22}} | |||
Der Eisverkäufer Hardy möchte seinen Kunden täglich frisches Eis verkaufen. Damit er immer die richtigen Mengen vorrätig hat und in Zukunft besser planen kann, zählt er an einem Tag bei 200 Kunden den Eiskugelkonsum: | Der Eisverkäufer Hardy möchte seinen Kunden täglich frisches Eis verkaufen. Damit er immer die richtigen Mengen vorrätig hat und in Zukunft besser planen kann, zählt er an einem Tag bei 200 Kunden den Eiskugelkonsum: | ||
| Zeile 1.258: | Zeile 1.170: | ||
* Wie viele Kugeln Eis kauften genau 35% der Kunden? | * Wie viele Kugeln Eis kauften genau 35% der Kunden? | ||
{{Loesung|Erdbeerplantage - Teil I|23}} | |||
Der Student Alois besitzt eine Erdbeerplantage in Bayern, um sich damit sein Studium zu finanzieren. Da das Ernteergebnis je nach “Qualität des Sommers” verschieden ist, notierte sich Alois, wie viele Stunden die Sonne in der diesjährigen Saison pro Tag auf seine Beeren einwirkte: | Der Student Alois besitzt eine Erdbeerplantage in Bayern, um sich damit sein Studium zu finanzieren. Da das Ernteergebnis je nach “Qualität des Sommers” verschieden ist, notierte sich Alois, wie viele Stunden die Sonne in der diesjährigen Saison pro Tag auf seine Beeren einwirkte: | ||
| Zeile 1.302: | Zeile 1.207: | ||
* An wie vielen Tagen in dieser Saison schien die Sonne prozentual 4 und 9 Stunden? | * An wie vielen Tagen in dieser Saison schien die Sonne prozentual 4 und 9 Stunden? | ||
{{Loesung|Erdbeerplantage - Teil II|24}} | |||
Der Student Alois, aus der Aufgabe [[Univariate Statistik/Aufgaben#Erdbeerplantage - Teil I|davor]], möchte wissen: | |||
* Wie viele Stunden schien die Sonne durchschnittlich pro Tag in der Saison? | |||
* Wie lange schien die Sonne höchstens an den 50% sonnenärmsten Tagen der Saison? | |||
{{Loesung|Festgeldkonten|25}} | |||
Eine internationale Bank, die in 5 Ländern agiert, bietet Festgeldkonten an. Die Einlagen werden länderabhängig mit einem variablen Zinssatz <math>z(L)=0,7z+0,3x_{0,5}(L)</math> verzinst, wobei <math>z(L)</math> der länderspezifische, variable Zinssatz, <math>z</math> ein länderunabhängiger Zinsatz und <math>x_{0,5}(L)</math> der Median der Zinssätze für Einlagen im jeweiligen Land sind. Der länderunabhängige Zinssatz <math>z</math> beträgt <math>5,2\%</math>. Die länderspezifischen Verteilungen der Einlagezinssätze sind in nachfolgender Tabelle gegeben: | Eine internationale Bank, die in 5 Ländern agiert, bietet Festgeldkonten an. Die Einlagen werden länderabhängig mit einem variablen Zinssatz <math>z(L)=0,7z+0,3x_{0,5}(L)</math> verzinst, wobei <math>z(L)</math> der länderspezifische, variable Zinssatz, <math>z</math> ein länderunabhängiger Zinsatz und <math>x_{0,5}(L)</math> der Median der Zinssätze für Einlagen im jeweiligen Land sind. Der länderunabhängige Zinssatz <math>z</math> beträgt <math>5,2\%</math>. Die länderspezifischen Verteilungen der Einlagezinssätze sind in nachfolgender Tabelle gegeben: | ||
| Zeile 1.351: | Zeile 1.259: | ||
Berechnen Sie den durchschnittlichen variablen Zinssatz für Festgeldkonten dieser internationalen Bank. | Berechnen Sie den durchschnittlichen variablen Zinssatz für Festgeldkonten dieser internationalen Bank. | ||
{{Loesung|Fließband|26}} | |||
An einem Fließband sind 6 Arbeiter acht Stunden am Tag mit der Kontrolle eines elektronischen Bauteils beschäftigt. Um ein Bauteil zu kontrollieren, benötigen sie folgende Zeiten: | An einem Fließband sind 6 Arbeiter acht Stunden am Tag mit der Kontrolle eines elektronischen Bauteils beschäftigt. Um ein Bauteil zu kontrollieren, benötigen sie folgende Zeiten: | ||
| Zeile 1.380: | Zeile 1.289: | ||
Berechnen Sie einen geeigneten Mittelwert für die Kontrollzeit pro Stück an diesem Fließband. | Berechnen Sie einen geeigneten Mittelwert für die Kontrollzeit pro Stück an diesem Fließband. | ||
{{Loesung|Führerschein–Entziehungen|27}} | |||
Promille gefährden den Führerschein! | Promille gefährden den Führerschein! | ||
| Zeile 1.407: | Zeile 1.317: | ||
* Berechnen Sie die Standardabweichung des Alters und den Variationskoeffizienten (runden Sie dafür das Durchschnittsalter auf ganze Jahre auf bzw. ab). | * Berechnen Sie die Standardabweichung des Alters und den Variationskoeffizienten (runden Sie dafür das Durchschnittsalter auf ganze Jahre auf bzw. ab). | ||
* In welchem Altersbereich liegen die mittleren 50% der betroffenen Fahrer(innen)? | * In welchem Altersbereich liegen die mittleren 50% der betroffenen Fahrer(innen)? | ||
* Welches Alter höchstens hatten die 50% jüngsten Fahrer(innen) mit Führerschein–Entzug? Welche | * Welches Alter höchstens hatten die 50% jüngsten Fahrer(innen) mit Führerschein–Entzug? Welche Maßzahl haben Sie berechnet? | ||
* Berechnen Sie zu der Ma“szahl unter d) ein geeignetes Streuungsma”s. | * Berechnen Sie zu der Ma“szahl unter d) ein geeignetes Streuungsma”s. | ||
{{Loesung|Gartenzwerg–Großhandel|28}} | |||
Herr Meier besitzt einen Gartenzwerg–Großhandel mit drei Filialen: Berlin, New York und Flensburg. Am Ende des Geschäftsjahres möchte er einen Überblick über die Geschäftslage erhalten und fordert deshalb in allen drei Filialen Informationen über die innerhalb des letzten Jahres eingegangenen Aufträge an. | Herr Meier besitzt einen Gartenzwerg–Großhandel mit drei Filialen: Berlin, New York und Flensburg. Am Ende des Geschäftsjahres möchte er einen Überblick über die Geschäftslage erhalten und fordert deshalb in allen drei Filialen Informationen über die innerhalb des letzten Jahres eingegangenen Aufträge an. | ||
| Zeile 1.417: | Zeile 1.328: | ||
<li><p>Seine Berliner Filiale übermittelt ihm folgende Informationen:</p> | <li><p>Seine Berliner Filiale übermittelt ihm folgende Informationen:</p> | ||
{|class="wikitable" | {|class="wikitable" | ||
!align="right"| Auftragshöhe in EUR | |||
|align="right"| | |align="right"| | ||
| Zeile 1.452: | Zeile 1.363: | ||
<li><p>Berechnen Sie die durchschnittliche Auftragshöhe für das gesamte Unternehmen.</p></li></ul> | <li><p>Berechnen Sie die durchschnittliche Auftragshöhe für das gesamte Unternehmen.</p></li></ul> | ||
{{Loesung|Gefahrene Strecke|29}} | |||
Bei 20 Vertretern eines Versicherungsunternehmens verteilt sich die in einer Woche mit dem Firmenwagen gefahrene Strecke wie folgt: | Bei 20 Vertretern eines Versicherungsunternehmens verteilt sich die in einer Woche mit dem Firmenwagen gefahrene Strecke wie folgt: | ||
{|class="wikitable" | |||
!Gefahrene Strecke in km | |||
0 | !Anzahl Vertreter | ||
50 | |- | ||
100 | |0-50 | ||
300 | |align="right"|3 | ||
500 | |- | ||
|50-100 | |||
|align="right"|5 | |||
|- | |||
|100-300 | |||
|align="right"|6 | |||
|- | |||
|300-500 | |||
|align="right"|4 | |||
|- | |||
|500-1000 | |||
|align="right"|2 | |||
|} | |||
Geben Sie die Länge des Bereiches an, in dem die 50% der Vertreter mit den mittleren gefahrenen Streckenlängen liegen. | |||
{{Loesung|Gleisbaubetrieb|30}} | |||
Der Direktor eines Gleisbaubetriebes erhält folgende Information: | Der Direktor eines Gleisbaubetriebes erhält folgende Information: | ||
| Zeile 1.475: | Zeile 1.399: | ||
Überprüfen Sie den angegebenen Mittelwert und korrigieren Sie ihn gegebenenfalls mit einer exakten Begründung. | Überprüfen Sie den angegebenen Mittelwert und korrigieren Sie ihn gegebenenfalls mit einer exakten Begründung. | ||
{{Loesung|Glücksspielautomaten|31}} | |||
In der Lieblingskneipe der Studentin Fritzi stehen zwei Glücksspielautomaten. Beide Automaten erwarten den gleichen Einsatz pro Spiel. Um ihre Gewinnchancen zu optimieren, spielt Fritzi mit jedem der Automaten für eine Weile. Folgende Gewinne erzielt sie in den einzelnen Spielen:<br /> | In der Lieblingskneipe der Studentin Fritzi stehen zwei Glücksspielautomaten. Beide Automaten erwarten den gleichen Einsatz pro Spiel. Um ihre Gewinnchancen zu optimieren, spielt Fritzi mit jedem der Automaten für eine Weile. Folgende Gewinne erzielt sie in den einzelnen Spielen:<br /> | ||
| Zeile 1.484: | Zeile 1.409: | ||
Welchen Median hat der Automat mit dem größten durchschnittlichen Gewinn? | Welchen Median hat der Automat mit dem größten durchschnittlichen Gewinn? | ||
{{Loesung|Grafische Darstellung|32}} | |||
Gegeben sind folgende Daten des statistischen Bundesamtes von 1998 über das Alter der im Straßenverkehr Getöteten innerhalb von Ortschaften. | |||
|align="right"| | {|class="wikitable" | ||
! Alter | |||
!align="right"| unter 15 | |||
!align="right"| 15 - 18 | |||
!align="right"| 18 - 25 | |||
!align="right"| 25 - 65 | |||
!align="right"| 65 - 90 | |||
|- | |||
| Anzahl | |||
|align="right"| 126 | |||
|align="right"| 76 | |||
|align="right"| 258 | |||
|align="right"| 808 | |||
|align="right"| 638 | |||
|} | |||
| | Welche der folgenden grafischen Darstellungen beschreibt die Häufigkeitsverteilung der Daten korrekt?<br /> | ||
<br /> | |||
[[File:Bild8.jpg|image]] | |||
{{Loesung|Intercity – Zug|33}} | |||
Ein Intercity – Zug legt 300 km in vier Abschnitten zurück, wobei die Geschwindigkeit wegen unterschiedlicher Streckenbeschaffenheit jeweils verschieden ist: | |||
{|class="wikitable" | |||
|align="center"| Streckenabschnitt | |||
|align="right"| Streckenlänge | |||
|align="right"| Geschwindigkeit | |||
|- | |- | ||
|align=" | |align="center"| | ||
|align="right"| | |align="right"| (in km) | ||
|align="right"| | |align="right"| (in km/h) | ||
|- | |- | ||
|align=" | |align="center"| A | ||
|align="right"| 100 | |||
|align="right"| 150 | |||
|align="right"| | |||
|align="right"| | |||
|- | |- | ||
|align=" | |align="center"| B | ||
|align="right"| 60 | |||
|align="right"| 120 | |||
|align="right"| | |||
|align="right"| | |||
|- | |- | ||
|align=" | |align="center"| C | ||
|align="right"| 50 | |||
|align="right"| 100 | |||
|align="right"| | |||
|align="right"| | |||
|- | |- | ||
|align=" | |align="center"| D | ||
|align="right"| 90 | |||
|align="right"| 90 | |||
|align="right"| | |||
|align="right"| | |||
|} | |} | ||
Berechnen Sie die Durchschnittsgeschwindigkeit für die Gesamtstrecke. | |||
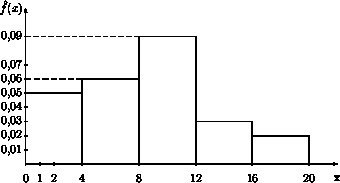
{{Loesung|Internetstunden|34}} | |||
Das folgende Histogramm gibt die Häufigkeitsverteilung von Internetstunden pro Woche für eine Grundgesamtheit von 100 Informatikstudenten an. | |||
[[File:Bild7.jpg|image]] | |||
Bestimmen Sie den Median aus diesen Daten. | |||
{{Loesung|Kaltmieten|35}} | |||
In einem Wohnviertel mit Häusern verschiedener Wohnungseigentümer sollen die Kaltmieten analysiert werden. Aus einer ersten Auswertung ergibt sich folgende Tabelle: | |||
== | {|class="wikitable" | ||
|align="right"| Kaltmiete (pro m<math>^2</math>) | |||
|align="right"| | |||
= | |||
|- | |- | ||
|align=" | |align="right"| von …bis unter … | ||
|align="right"| Anzahl | |||
|align="right"| | |- | ||
|align="right"| | |align="right"| 0–6 | ||
|align="right"| 5 | |||
|- | |||
|align="right"| 6–8 | |||
|align="right"| 10 | |||
|- | |- | ||
|align="right"| 8–10 | |||
|align="right"| | |align="right"| 30 | ||
|align="right"| | |||
|- | |- | ||
|align="right"| 10–13 | |||
|align="right"| | |align="right"| 30 | ||
|align="right"| | |||
|- | |- | ||
|align="right"| 13–16 | |||
|align="right"| | |align="right"| 20 | ||
|align="right"| | |||
|- | |- | ||
|align="right"| 16–20 | |||
|align="right"| | |align="right"| 5 | ||
|align="right"| | |||
|} | |} | ||
Bestimmen Sie den Median aus diesen Daten. | |||
{{Loesung|Kartoffeln|36}} | |||
An zwei Verladestellen für Kartoffeln der Deutschen Bahn wurden folgende Angaben ermittelt: | |||
{|class="wikitable" | |||
|align="right"| Verlade- | |||
|align="right"| Kosten gesamt | |||
|align="right"| Kosten je | |||
|align="right"| Kosten je verladene Tonne | |||
|- | |||
|align="right"| stelle | |||
|align="right"| (EUR) | |||
|align="right"| Stunde (EUR/h) | |||
|align="right"| (EUR/t) | |||
|- | |||
|align="right"| 1 | |||
|align="right"| 16 000 | |||
|align="right"| 40 | |||
|align="right"| 1,00 | |||
|- | |||
|align="right"| 2 | |||
|align="right"| 27 000 | |||
|align="right"| 45 | |||
|align="right"| 0,75 | |||
|} | |||
* Berechnen Sie die durchschnittlichen Kosten je verladene Tonne der beiden Verladestellen. | |||
* Wieviel Tonnen wurden durchschnittlich je Stunde bei beiden Verladestellen verladen? | |||
{{Loesung|Kaufkurs der Aktien|37}} | |||
Zu Börsenbeginn am gestrigen Tag betrug der Kurs von 4 Aktien, die in Zeile 2 der Tabelle angegebenen Werte. Jemand kaufte zu diesen Kursen die Aktien zu den Kaufbeträgen, die in der Zeile 3 der Tabelle enthalten sind. | |||
{|class="wikitable" | |||
! Aktie | |||
!align="right"| A | |||
!align="right"| B | |||
!align="right"| C | |||
!align="right"| D | |||
|- | |- | ||
|align="right"| | | Kurs (in Euro) | ||
|align="right"| | |align="right"| 500 | ||
|align="right"| 600 | |||
|align="right"| | |align="right"| 400 | ||
|align="right"| | |align="right"| 700 | ||
|- | |- | ||
| | | Kaufbetrag (in Euro) | ||
|align="right"| 45000 | |||
|align="right"| 84000 | |||
|align="right"| 3600 | |||
|align="right"| 14000 | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|} | |} | ||
Berechnen Sie den mittleren Kaufkurs der Aktien. | |||
{{Loesung|Körperschaftssteueraufkommen|38}} | |||
Über das Körperschaftssteueraufkommen einer Stadt, angegeben nach den Rechtsformen der körperschaftssteuerpflichtigen Gesellschaften, sind nachstehende Maßzahlen bekannt: | |||
{| | {|class="wikitable" | ||
| Rechtsform | |||
|align="right"| | |align="right"| steuer- | ||
|align="right"| | |align="right"| mittleres Steuer- | ||
|align="right"| | |align="right"| Standard- | ||
|- | |- | ||
| | | | ||
|align="right"| | |||
|align="right"| | |align="right"| pflichtige | ||
|align="right"| | |align="right"| aufkommen | ||
|align="right"| abweichung | |||
|- | |- | ||
| | | | ||
|align="right"| | |||
|align="right"| | |align="right"| Fälle | ||
|align="right"| | |align="right"| (TEUR) | ||
|align="right"| (TEUR) | |||
|- | |- | ||
|align="right"| | | AG, KGaA | ||
|align="right"| | |align="right"| 100 | ||
|align="right"| | |align="right"| 9500 | ||
|align="right"| | |align="right"| 1000 | ||
|- | |||
| GmbH | |||
|align="right"| 9500 | |||
|align="right"| 100 | |||
|align="right"| 80 | |||
|- | |||
| eG | |||
|align="right"| 300 | |||
|align="right"| 200 | |||
|align="right"| 100 | |||
|- | |||
| sonstige | |||
|align="right"| 100 | |||
|align="right"| 400 | |||
|align="right"| 250 | |||
|} | |} | ||
Berechnen Sie die Standardabweichung des Körperschaftssteueraufkommens für die gesamte Stadt. | |||
{{Loesung|Kontrollzeiten|39}} | |||
An einem Fließband sind sechs Arbeiterinnnen acht Stunden am Tag mit der Kontrolle eines elektronischen Bauteils beschäftigt. Um ein Bauteil zu kontrollieren, benötigen sie folgende Zeiten: | |||
{| | {|class="wikitable" | ||
! | ! Arbeiterin | ||
!align="right"| | !align="right"| Stückzeit | ||
|- | |||
| Frau Arbeitsam | |||
|align="right"| 0,2 min | |||
|- | |||
| Frau Beeilung | |||
|align="right"| 0,4 min | |||
|- | |||
| Frau Chaos | |||
|align="right"| 0,8 min | |||
|- | |||
| Frau Durchschnitt | |||
|align="right"| 0,5 min | |||
|- | |- | ||
| | | Frau Emsig | ||
|align="right"| | |align="right"| 0,5 min | ||
|- | |- | ||
| | | Frau Faultier | ||
|align="right"| | |align="right"| 0,8 min | ||
|} | |} | ||
Berechnen Sie | Berechnen Sie die durchschnittliche Kontrollzeit pro Stück an diesem Fließband. | ||
{{Loesung|Kurzarbeiter|40}} | |||
Im März wurden in den fünf neuen Bundesländern folgende Anzahlen von Kurzarbeitern nach dem Arbeitsausfall (in %) registriert (fikitve Daten): | |||
{|class="wikitable" | |||
!align="right"| Arbeitsausfall (%) | |||
!align="right"| Anzahl der Kurzarbeiter | |||
|- | |||
|align="right"| 10 – 25 | |||
|align="right"| 461 200 | |||
|- | |||
|align="right"| 25 – 50 | |||
|align="right"| 687 400 | |||
|- | |||
|align="right"| 50 – 75 | |||
|align="right"| 385 200 | |||
|- | |||
|align="right"| 75 – 100 | |||
|align="right"| 233 200 | |||
|} | |||
* Berechnen Sie den durchschnittlichen Arbeitsausfall der Kurzarbeiter im März in den fünf neuen Bundesländern. | |||
* Welcher Arbeitsausfall ergibt sich, wenn 50% der Kurzarbeiter einen geringeren Arbeitsausfall und 50% der Kurzarbeiter einen höheren Arbeitsausfall hatten? | |||
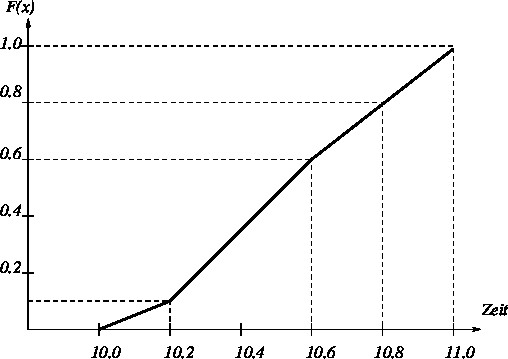
{{Loesung|Leichtathletikabteilung|41}} | |||
Die Leichtathletikabteilung des Sportvereins Z ist spezialisiert auf das Training von 100 m – LauferInnen. Nach einem Jahr intensivsten Trainings wurden die Zeiten der 20 LäuferInnen des Vereins gestoppt. Dabei ergab sich folgende Verteilungsfunktion: | |||
[[File:Bild4.jpg|image]] | |||
* Zeichnen Sie die zur Verteilungsfunktion gehörige Häufigkeitsverteilung. | |||
* Welche Zeit höchstens benötigen die 80% schnellsten Läufer? | |||
* Berechnen Sie die mittlere quadratische Abweichung bezogen auf das arithmetische Mittel und auf den Median. | |||
* Welche Grö“senbeziehung besteht zwischen den beiden Ergebnissen von c)? Gilt diese Grö”senbeziehung stets? Wenn ja, zeigen Sie dies. | |||
{{Loesung|Lernzeit|42}} | |||
Ein Universitätspräsident gibt eine statistische Untersuchung in Auftrag, mit der festgestellt werden soll, wie viel Zeit die Studierenden für ihr Studium aufwenden. Die Befragung von 100 Studierenden dieser Universität brachte folgendes Ergebnis:<br /> | |||
Keiner der Befragten lernt 12 und mehr Stunden am Tag. Bei 22 Studierenden wurde festgestellt, dass sie sich mindestens 6 Stunden am Tag mit ihrem Studium beschäftigen. Weniger als 3 Stunden am Tag investierten 30% der Befragten in ihr Studium. Die Masse der Studierenden (65%) beschäftigt sich zwischen 3 und 8 Stunden täglich mit Studienangelegenheiten. | |||
* Wie heißt das untersuchte Merkmal und wie ist es skaliert? | |||
* Bestimmen Sie tabellarisch die absoluten und relativen Häufigkeiten und die empirische Verteilungsfunktion. Teilen Sie zu diesem Zweck die Daten in vier Klassen ein. | |||
* Wie viele Stunden höchstens beschäftigt sich genau die Hälfte der Befragten täglich mit dem Studium? | |||
* Wie viele der Befragten arbeiten mindestens 5 Stunden täglich für ihr Studium? | |||
* Wie groß ist der durchschnittliche Zeitaufwand für das Studium bei den 100 befragten Studierenden? | |||
* Welcher Zeitaufwand für das Studium trat bei den befragten Studierenden am häufigsten auf? | |||
{{Loesung|Lineares Streuungsmaß|43}} | |||
Von den der Größe nach aufsteigend geordneten fünf Werten eines Merkmals X sind nur die ersten vier lesbar: | |||
| | {| | ||
|align="right"| 3 | |||
|align="right"| 7 | |||
|align="right"| 17 | |||
|align="right"| 19 | |||
|align="right"| ?? | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|} | |} | ||
Wie lautet der 5. Wert, wenn bekannt ist, dass die durchschnittliche absolute Abweichung (lineares Streuungsmaß) der fünf Werte – bezogen auf den Median – gleich 8 ist? | |||
{{Loesung|Maschinen|44}} | |||
In einer Fabrik stehen zwei Maschinen, die Motorenhauben stanzen: die erste Maschine für den Fiat mit einer durchschnittlichen Länge von 80 cm, die zweite für den Mercedes mit einer durchschnittlichen Länge von 300 cm. Die erste Maschine produziert mit einer Standardabweichung von 4 cm, die zweite mit einer Standardabweichung von 6 cm. | |||
Welche Maschine arbeitet zuverlässiger? | |||
{{Loesung|Miete und Wohnfläche|45}} | |||
{| | In einem Wohnviertel mit Häusern verschiedener Wohnungseigentümer wird die Quadratmetermiete in Abhängigkeit von der Wohnfläche analysiert. Es ergibt sich aus der Auswertung von 10 Mietwohnungen folgendes Bild: | ||
{|class="wikitable" | |||
|align="right"| Wohnfläche (m<math>^2</math>) | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
= | |align="right"| | ||
|align="right"| | |||
|- | |- | ||
|align="right"| | |align="right"| <math>x_i</math> | ||
|align="right"| | |align="right"| | ||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
= | |align="right"| | ||
|- | |||
|align="right"| 40 | |||
|align="right"| 12 | |||
|align="right"| 12 | |||
|align="right"| 15 | |||
|align="right"| | |||
|- | |||
|align="right"| 60 | |||
|align="right"| 12 | |||
|align="right"| | |||
|align="right"| | |||
= | |align="right"| | ||
|- | |||
|align="right"| 80 | |||
|align="right"| 10 | |||
|align="right"| 10 | |||
|align="right"| | |||
|align="right"| | |||
|- | |||
|align="right"| 90 | |||
|align="right"| 9 | |||
|align="right"| 10 | |||
|align="right"| 10 | |||
|align="right"| | |align="right"| 10 | ||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|} | |} | ||
Der Makler möchte wissen, wie die Abhängigkeit von Miete und Wohnfläche ist. Bestimmen Sie für ihn die Kovarianz der Merkmale. | |||
{{Loesung|Minimale Summe|46}} | |||
Für ein metrisches Merkmal hat man folgende Urliste | |||
=== | {|class="wikitable" | ||
!align="center"| <math>i</math> | |||
!align="right"| 1 | |||
!align="right"| 2 | |||
!align="right"| 3 | |||
! | !align="right"| 4 | ||
!align="right"| | !align="right"| 5 | ||
!align="right"| | !align="right"| 6 | ||
!align="right"| 7 | |||
!align="right"| 8 | |||
|- | |- | ||
|align="center"| <math>x_i</math> | |||
|align=" | |||
|align="right"| 5 | |align="right"| 5 | ||
|align="right"| | |align="right"| 7 | ||
|align="right"| 9 | |||
|align="right"| 10 | |||
|align="right"| 10 | |||
|align="right"| 12 | |||
|align="right"| 13 | |||
|align="right"| 14 | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|} | |} | ||
Für welche reelle Zahl <math>c</math> ist <math>\sum_{i=1}^8(x_i-c)^2</math> minimal? (ohne Beweis!) | |||
{{Loesung|Nelkenstrauß|47}} | |||
Ein Kunde kauft an einem Tag einen Strau“s Nelken für 12 EUR, das Stück zu 0,80 EUR, und am nächsten Tag einen Strau”s Nelken für 26 EUR, das Stück zu 1,04 EUR. Welcher durchschnittliche Preis ist für eine Nelke an diesen beiden Tagen bezahlt worden? | |||
{{Loesung|Neubauwohnungen|48}} | |||
Über die Bauzeiten der im Jahre in der Stadt C errichteten Neubauwohnungen liegen folgende Angaben vor:<br /> | |||
{|class="wikitable" | |||
|align="right"| <span>Bauzeit</span> | |||
|align="right"| Anteil der neugebauten | |||
|- | |- | ||
|align="right"| < | |align="right"| <span>(in Monaten)</span> | ||
|align="right"| | |align="right"| Wohnungseinheiten (in Prozent) | ||
|- | |- | ||
|align="right"| | |align="right"| 2–4 | ||
|align="right"| | |align="right"| 3,7 | ||
|- | |- | ||
|align="right"| | |align="right"| 4–6 | ||
|align="right"| | |align="right"| 13,1 | ||
|align="right"| | |- | ||
|align="right"| 6–8 | |||
|align="right"| 27,5 | |||
|- | |||
|align="right"| 8–10 | |||
|align="right"| 21,1 | |||
|- | |||
|align="right"| 10–12 | |||
|align="right"| 16,0 | |||
|- | |||
|align="right"| 12–14 | |||
|align="right"| 6,4 | |||
|- | |||
|align="right"| 14–16 | |||
|align="right"| 5,3 | |||
|- | |||
|align="right"| 16–18 | |||
|align="right"| 6,9 | |||
|} | |||
Berechnen Sie drei aussagekräftige Mittelwerte zur Beantwortung der Frage: | |||
Wie viele Monate Bauzeit wurden im Mittel für die im Jahre in der Stadt C errichteten Wohnungseinheiten benötigt? | |||
| | {{Loesung|Perlenkette|49}} | ||
Agathe hat von ihrem Freund eine Perlenkette geschenkt bekommen. Um sich einen Überblick über den Wert der Kette zu verschaffen, misst sie die Durchmesser (in mm) der Perlen: | |||
{|class="wikitable" | |||
|align="right"| 3,1 | |||
|align="right"| 4,2 | |||
|align="right"| 3,7 | |||
|align="right"| 6,8 | |||
|align="right"| 7,3 | |||
|align="right"| 5,2 | |||
|align="right"| 5,4 | |||
|align="right"| 4,5 | |||
|align="right"| 3,9 | |||
|align="right"| 3,3 | |||
|- | |- | ||
|align="right"| | |align="right"| 5,0 | ||
|align="right"| 9 | |align="right"| 3,7 | ||
|align="right"| | |align="right"| 6,9 | ||
|align="right"| | |align="right"| 6,1 | ||
|align="right"| | |align="right"| 4,0 | ||
| | |align="right"| 4,1 | ||
|align="right"| 6,1 | |||
|align="right"| 6,0 | |||
|align="right"| 5,7 | |||
= | |align="right"| 5,2 | ||
|- | |||
|align="right"| 5,6 | |||
|align="right"| 4,4 | |||
|align="right"| 4,2 | |||
|align="right"| 3,7 | |||
|align="right"| 5,3 | |||
|align="right"| 3,4 | |||
|align="right"| 6,8 | |||
|align="right"| 6,3 | |||
|align="right"| 4,1 | |||
|align="right"| 3,3 | |||
|- | |- | ||
|align=" | |align="right"| 4,2 | ||
|align="right"| 5 | |align="right"| 5,8 | ||
|align="right"| | |align="right"| 5,6 | ||
|align="right"| | |align="right"| 3,2 | ||
|align="right"| | |align="right"| 5,5 | ||
|align="right"| | |align="right"| 4,5 | ||
|align="right"| | |align="right"| 5,1 | ||
|align="right"| | |align="right"| 4,6 | ||
|align="right"| | |align="right"| 5,3 | ||
|align="right"| 3,4 | |||
|align="right"| | |||
|- | |- | ||
|align="right"| | |align="right"| 6,5 | ||
|align="right"| | |align="right"| 6,2 | ||
| | |align="right"| 4,0 | ||
|align="right"| | |align="right"| 3,6 | ||
|align="right"| | |align="right"| 4,9 | ||
|align="right"| 4,8 | |||
|align="right"| 4,9 | |||
|align="right"| 4,6 | |||
|align="right"| 4,7 | |||
|align="right"| 4,8 | |||
|- | |- | ||
|align="right"| | |align="right"| 4,5 | ||
|align="right"| | |align="right"| 5,4 | ||
|align="right"| 3,5 | |||
|align="right"| 5,8 | |||
|align="right"| 4,9 | |||
|align="right"| 5,0 | |||
|align="right"| 3,6 | |||
|align="right"| 7,5 | |||
|align="right"| 3,2 | |||
|align="right"| 3,2 | |||
|- | |- | ||
|align="right"| | |align="right"| 3,4 | ||
|align="right"| | |align="right"| 3,5 | ||
|align="right"| 3,2 | |||
|align="right"| 5,1 | |||
|align="right"| 5,5 | |||
|align="right"| 4,3 | |||
|align="right"| 4,5 | |||
|align="right"| 3,8 | |||
|align="right"| 5,1 | |||
|align="right"| 3,8 | |||
|- | |- | ||
|align="right"| | |align="right"| 7,2 | ||
|align="right"| 5,9 | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
= | |align="right"| | ||
|align="right"| | |||
|align="right"| | |||
= | |align="right"| | ||
|} | |||
{| | * Erstellen Sie eine Häufigkeitstabelle bei Zugrundelegung von Klassen mit 1 mm Klassenbreite. | ||
* Berechnen Sie basierend auf den klassierten Daten den durchschnittlichen Durchmesser der Perlen. | |||
| | * Welcher Durchmesser trat bei dieser Perlenkette am häufigsten auf? | ||
* Welchen Durchmesser höchstens haben 50% der kleinsten Perlen? | |||
{{Loesung|Produktionsleistung einer Maschine|50}} | |||
An einer neu angeschafften Maschine, die pro Tag maximal 300 Produkteinheiten herstellen kann, werden an insgesamt 20 Tagen folgende Stückzahlen produziert: | |||
{|class="wikitable" | |||
!align="right"| Anzahl der Tage | |||
!align="right"| 6 | |||
!align="right"| 3 | |||
!align="right"| 5 | |||
!align="right"| 4 | |||
!align="right"| 2 | |||
|- | |- | ||
|align="right"| | |align="right"| produzierte Stück/Tag | ||
|align="right"| | |align="right"| 296 | ||
|align="right"| | |align="right"| 297 | ||
|align="right"| | |align="right"| 298 | ||
|align="right"| | |align="right"| 295 | ||
|align="right"| | |align="right"| 299 | ||
| | |} | ||
* Der Abteilungsleiter behauptet gegenüber dem Firmenchef, dass die Maschine im Durchschnitt pro Tag über 98% ihrer Produktionsleistung erbringt. Überprüfen Sie diese Aussage! | |||
* Berechnen Sie den Median und die mittlere absolute Abweichung vom Median der produzierten Stückzahlen/Tag. | |||
|- | |||
| | {{Loesung|Reinigungsunternehmen - Teil I|51}} | ||
| | |||
Für die Angestellten der drei Putzkolonnen eines Reinigungsunternehmens ergeben sich aufgrund von Alter, Betriebszugehörigkeit und Einsatzgebiet folgende Einkommen (in EUR) pro Monat: | |||
| | * 2 624, 2 830, 2 386, 2 395, 2 147, 2 546 | ||
* 2 936, 2 758, 2 774, 2 822 | |||
* 2 325, 2 536, 2 395, 2 454, 2 640. | |||
Berechnen Sie für jede Putzkolonne und für das gesamte Reinigungsunternehmen das durchschnittliche Einkommen und den Median des Einkommens. | |||
{{Loesung|Reinigungsunternehmen - Teil II|52}} | |||
Berechnen Sie für jede Putzkolonne aus der Aufgabe [[Univariate Statistik/Aufgaben#Reinigungsunternehmen - Teil I|davor]] die Standardabweichung und den Variationskoeffizienten. | |||
Ermitteln Sie anschließend unter Verwendung dieser Varianzen die Varianz des zusammengesetzten Datensatzes, d.h. die Varianz für das gesamte Reinigungsunternehmen. | |||
{{Loesung|Sanatorium|53}} | |||
In einem Sanatorium wird ein kleiner Wettlauf der Patienten über 50m durchgeführt. Die folgende Tabelle gibt in der Reihenfolge ihres Eintreffens am Ziel das Gewicht (in kg) der Patienten an: | |||
{|class="wikitable" | |||
!align="right"| Patient | |||
!align="right"| 1 | |||
!align="right"| 2 | |||
!align="right"| 3 | |||
!align="right"| 4 | |||
!align="right"| 5 | |||
!align="right"| 6 | |||
!align="right"| 7 | |||
!align="right"| 8 | |||
!align="right"| 9 | |||
!align="right"| 10 | |||
!align="right"| 11 | |||
|- | |- | ||
|align="right"| | |align="right"| Gewicht | ||
|align="right"| | |align="right"| 70 | ||
|align="right"| | |align="right"| 60 | ||
|align="right"| | |align="right"| 80 | ||
|align="right"| | |align="right"| 77 | ||
|align="right"| | |align="right"| 82 | ||
|align="right"| | |align="right"| 81 | ||
|align="right"| | |align="right"| 78 | ||
|align="right"| | |align="right"| 100 | ||
|align="right"| | |align="right"| 83 | ||
|align="right"| 110 | |||
|align="right"| | |align="right"| 79 | ||
|align="right"| | |} | ||
| | |||
* Wie stark ist der Zusammenhang zwischen Körpergewicht und Laufleistung? | |||
* Bestimmen Sie den Median des Körpergewichts. | |||
* Bestimmen Sie das quadratische Streuungsmaß in Bezug auf den Median. | |||
* Ist die Varianz des Gewichts grö“ser oder kleiner als die unter c) bestimmte Grö”se? Warum? | |||
* Die zwei Frauen unter den Patienten liefen die Strecke mit Geschwindigkeiten von 2 bzw. 4 Meter pro Sekunde. Wie groß war die Durchschnittsgeschwindigkeit der Frauen? | |||
{{Loesung|Schafzucht - Teil I|54}} | |||
|- | |||
Der schottische Großgrundbesitzer McDuff verdient sein Geld mit der Zucht von Schafen. Er nimmt sich für die nächste Schafsschur vor, sowohl billige irische Wanderarbeiter mit einem Leistungslohn von 15 Pfund pro kg Wolle, als auch einheimische Arbeiter für 20 Pfund pro kg Wolle einzusetzen. Für die Iren will er insgesamt 285 Pfund, für die Schotten insgesamt 260 Pfund an Lohnsumme aufbringen. | |||
Wie hoch sind seine durchschnittlichen Lohnkosten pro kg Wolle? | |||
| | {{Loesung|Schafzucht Teil - II|55}} | ||
| | Fortsetzung der Aufgabe [[Univariate Statistik/Aufgaben#Schafzucht - Teil I|davor]]. Unser schottischer Großgrundbesitzer McDuff (aus Aufgabe 33) verkauft die Wolle an einen Freund auf den Niederländischen Antillen. Im Laufe der letzten fünf Monate erwirtschaftete er folgende Gewinne (in Tsd. Gulden): 5 ; 4 ; 20 ; 6 ; 4. | ||
McDuff tauscht sein Geld stets bei einem Bankier in Edinburgh in Pfund ein. Er weiß, dass der Wechselkurs stabil ist und er jeden Monat eine feste, vom Umtauschbetrag unabhängige Gebühr zu entrichten hat. In den letzten fünf Monaten hat er insgesamt 15,5 (Tsd.) Pfund ausgezahlt bekommen. Die Varianz betrug 9,44 (Tsd. Pfund)<math>^{\rm 2}</math>. | |||
Wie hoch sind Gebühr und Wechselkurs? | |||
|} | {{Loesung|Schulbezirke|56}} | ||
Aus einem Datensatz mit nicht klassierten Daten über 506 Schulbezirke in einer Großstadt wurden folgende Variablen zur Analyse ausgewählt: | |||
* <math>X</math>: der Schulbezirk liegt verkehrsgünstig (1) oder nicht (0) | |||
* <math>Y</math>: durchschnittliche Anzahl von Räumen pro Haus im Schulbezirk | |||
Für diese Variablen wurden folgende Maßzahlen berechnet: | |||
{| | {|class="wikitable" | ||
! Maßzahl | |||
!align="right"| | !align="right"| <math>X</math> | ||
!align="right"| | !align="right"| <math>Y</math> | ||
|- | |||
| arithmetischer Mittelwert | |||
|align="right"| 0,07 | |||
|align="right"| 6,28 | |||
|- | |- | ||
| | | Maximum | ||
|align="right"| | |align="right"| 1,00 | ||
|align="right"| 8,78 | |||
|- | |- | ||
|align="right"| | | Median | ||
|align="right"| | |align="right"| 0,00 | ||
|align="right"| | |align="right"| 6,21 | ||
|align="right"| | |- | ||
|align="right"| | | Minimum | ||
|align="right"| | |align="right"| 0,00 | ||
|align="right"| | |align="right"| 3,56 | ||
|align="right"| | |- | ||
|align="right"| | | Modus | ||
|align="right"| | |align="right"| 0,00 | ||
|align="right"| | |align="right"| 5,71 | ||
|align="right"| | |- | ||
| | | Spannweite | ||
|align="right"| 1,00 | |||
|align="right"| 5,22 | |||
|- | |||
| Standardabweichung | |||
|align="right"| 0,00 | |||
|align="right"| 0,70 | |||
|- | |||
| Varianz | |||
|align="right"| 0,07 | |||
|align="right"| 0,49 | |||
|- | |||
| 25%-Quartil | |||
|align="right"| 0,00 | |||
|align="right"| 5,88 | |||
|- | |||
| 75%-Quartil | |||
|align="right"| 0,00 | |||
|align="right"| 6,63 | |||
|} | |||
Begründen Sie kurz, welche Maßzahlen für welche Variable sinnvoll sind. | |||
{{Loesung|Streuungsmaß|57}} | |||
Gegeben sind <math>n=50</math> Beobachtungswerte <math>x_1,x_2,\dots,x_{50}</math> eines Merkmals X. Zur Konstruktion eines Streuungsmaßes sollen die absoluten (d.h. ohne Berücksichtigung des Vorzeichens) Abweichungen eines jeden Beobachtungswertes von jedem anderen Beobachtungswert ermittelt werden. | |||
* Wie groß ist die Anzahl der zu ermittelnden absoluten Abweichungen? Begründen Sie diese Anzahl mittels der Kombinatorik. | |||
* Welche Skalierung ist für das Merkmal X erforderlich, um ein solches Streuungsmaß zu konstruieren? | |||
{{Loesung|Tägliche Arbeitswege - Teil I|58}} | |||
Der Direktor einer Bank möchte sich über die täglich anfallenden Anfahrtswege seiner Mitarbeiter zum Arbeitsplatz informieren. Von der Personalabteilung wird ihm auf seine Anfrage folgende Tabelle übersandt. | |||
{|class="wikitable" | |||
|align="right"| Anfahrtsweg (km) | |||
|align="right"| Anzahl der | |||
|- | |||
|align="right"| | |||
|align="right"| Beschäftigten | |||
|- | |||
|align="right"| 0 – 1 | |||
|align="right"| 7 | |||
|- | |- | ||
|align="right"| 1 – 5 | |||
|align="right"| | |align="right"| 24 | ||
|align="right"| | |||
|- | |- | ||
|align="right"| 5 – 15 | |||
|align="right"| | |align="right"| 35 | ||
|align="right"| | |||
|- | |- | ||
|align="right"| 15 – 30 | |||
|align="right"| | |align="right"| 18 | ||
|align="right"| | |||
|- | |- | ||
|align="right"| 30 – 50 | |||
|align="right"| | |align="right"| 16 | ||
|align="right"| | |} | ||
| | |||
* Nennen Sie die statistischen Einheiten und das untersuchte statistische Merkmal. Wie ist das Merkmal skaliert? | |||
* Ermitteln Sie die absoluten und relativen Häufigkeiten, die Häufigkeitsdichten und die empirische Verteilungsfunktion. Stellen Sie die Häufigkeitsverteilung und die empirische Verteilungsfunktion graphisch dar. | |||
* Berechnen Sie den durchschnittlichen Anfahrtsweg. | |||
* Welcher Anfahrtsweg tritt bei den Beschäftigten dieser Bank am häufigsten auf? Wie wird dieser Parameter genannt? | |||
* Welcher Anfahrtsweg ergibt sich, wenn 50% der Beschäftigten einen kürzeren bzw. 50% einen weiteren Anfahrtsweg haben? | |||
* Berechnen Sie die p–Quantile für <math>p \in \{ 0,05, 0,25, 0,75, 0,9\}</math>. | |||
{{Loesung|Tägliche Arbeitswege - Teil II|59}} | |||
Berechnen Sie, ausgehend von der Aufgabe [[Univariate Statistik/Aufgaben#Schafzucht - Teil I|davor]] | |||
* den Quartilsabstand | |||
* die mittlere absolute Abweichung vom Median | |||
des Anfahrtsweges/Beschäftigter der betrachteten Bank. | |||
{{Loesung|Tarifverhandlungen|60}} | |||
Ein Großunternehmen veröffentlicht folgende Angaben über die Verteilung der Jahresbruttolöhne seiner Lohnempfänger im Jahre 2011: Von den insgesamt 20000 Lohnempfängern bezogen 16000 einen Jahresbruttolohn von mindestens 9600 EUR. Der durchschnittliche Jahresbruttolohn betrug 21200 EUR.<br /> | |||
Bei den nächsten Tarifverhandlungen wird folgendes vereinbart: Alle Lohnempfänger erhalten 5% mehr Bruttolohn. Weiter erhalten alle Lohnempfänger mit einem bisherigen Bruttolohn unter 9600 EUR zusätzlich einen Festbetrag von jährlich 200 EUR mehr.<br /> | |||
Unterstellen Sie, dass außer den vereinbarten Tarifänderungen keine weiteren Anderungen (Zahl und Struktur der Lohnempfänger, Klasseneinteilung) eintreten.<br /> | |||
Wie groß ist dann der durchschnittliche Jahresbruttolohn nach dem Tarifabschluß? | |||
{{Loesung|Tekolom und IBBM - Teil I|61}} | |||
Herr Sparsam besaß im letzten Jahr Aktien der Firma Tekolom und IBBM. Für die beiden Aktien ist die folgende gemeinsame Häufigkeitsverteilung beobachtet worden: | |||
{|class="wikitable" | |||
|align="right"| Anzahl | |||
|align="right"| Kurs der | |||
|align="right"| Kurs der | |||
|- | |||
|align="right"| der Tage | |||
|align="right"| Tekolom-Aktie | |||
|align="right"| IBBM-Aktie | |||
|- | |||
|align="right"| 73 | |||
|align="right"| 35 EUR | |||
|align="right"| 120 EUR | |||
|- | |||
|align="right"| 146 | |||
|align="right"| 40 EUR | |||
|align="right"| 130 EUR | |||
|- | |||
|align="right"| 146 | |||
|align="right"| 45 EUR | |||
|align="right"| 125 EUR | |||
|} | |||
Stellen Sie fest, ob die Kurse der beiden Aktien korreliert sind. Berechnen Sie den Korrelationskoeffizienten nach Bravais–Pearson. | |||
{{Loesung|Telefonanbieter|62}} | |||
Familie Sparsam nutzt fleißig die Niedrigpreise verschiedener Telefonanbieter. Im Monat Februar 2015 ergibt ihre Telefonrechnung folgende Daten für Ferngespräche: | |||
{|class="wikitable" | |||
| Anbieter | |||
|align="right"| Minutenpreis | |||
|align="right"| Rechnungsbetrag | |||
|- | |- | ||
| | | | ||
|align="right"| | |align="right"| (in EUR) | ||
|align="right"| (in EUR) | |||
|align="right"| | |||
|- | |- | ||
| | | <math>A_1</math> | ||
|align="right"| | |align="right"| 0,10 | ||
|align="right"| 20 | |align="right"| 20,00 | ||
|align="right"| | |- | ||
| <math>A_2</math> | |||
|align="right"| 0,15 | |||
|align="right"| 11,25 | |||
|- | |- | ||
| | | <math>A_3</math> | ||
|align="right"| | |align="right"| 0,19 | ||
|align="right"| | |align="right"| 47,50 | ||
|} | |} | ||
Berechnen Sie den von Familie Sparsam im Februar bezahlten Durchschnittspreis für eine Minute Ferngespräch. | |||
{{Loesung|Telefon–Interviews|63}} | |||
Eine Marketing-Firma führt häufig Telefon-Interviews in Berlin durch. Hierbei werden folgende Entgelte an die Telekom bezahlt: im Tagestarif (9-18 Uhr) 12 Cent/90 Sekunden und im Freizeittarif (5-9 Uhr und 18-21 Uhr) 12 Cent/150 Sekunden.<br /> | |||
Es soll ausdrücklich darauf hingewiesen werden, dass bei der Telekom jede angefangene 90– bzw. 150–Sekundeneinheit voll bezahlt werden muss.<br /> | |||
Die Interviews dauern entweder genau 10 oder genau 20 Minuten. An einem zufällig ausgewählten Tag werden die Telefongespräche wie folgt geführt: | |||
=== | {|class="wikitable" | ||
!align="right"| Zeitbereich | |||
!align="right"| 10-Min.-Interviews | |||
!align="right"| 20-Min.-Interviews | |||
|- | |||
|align="right"| 7-8 Uhr | |||
|align="right"| 3 | |||
|align="right"| 1 | |||
|- | |||
|align="right"| 11-14 Uhr | |||
|align="right"| 10 | |||
|align="right"| 20 | |||
|- | |||
|align="right"| 19-20 Uhr | |||
|align="right"| 15 | |||
|align="right"| 10 | |||
|} | |||
Wie hoch sind die mittleren Telefonkosten für ein Interview an diesem Tag? | |||
{{Loesung|Tennis Turniere|64}} | |||
Tennis–As B.B. blickt auf eine völlig missglückte Saison zurück. Insgesamt nahm er an 40 Turnieren in aller Welt teil. Jedes Turnier ging über 6 Runden: | |||
1. Runde<br /> | |||
2. Runde<br /> | |||
3. Runde = Achtelfinale<br /> | |||
4. Runde = Viertelfinale<br /> | |||
5. Runde = Halbfinale<br /> | |||
6. Runde = Finale | |||
Gespielt wurde in jeder Runde im k.o.–Verfahren, d.h. der Spieler, der seine Partie verlor, schied aus. | |||
Die Bilanz seiner Turnierergebnisse lässt keine Freude bei B.B. aufkommen: Er stand zweimal im Finale und wurde sechsmal erst im Halbfinale von seinem Gegner geschlagen. Zehnmal verlor er jedoch schon in der ersten Runde und sechzehnmal kam für ihn in der 2. Runde das Aus. In der dritten Runde schied er allerdings bei keinem Turnier aus. | |||
= | * Wie heißt das untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret? | ||
* Bestimmen Sie tabellarisch die absoluten und relativen Häufigkeiten und die empirische Verteilungsfunktion. | |||
* Zeichnen Sie die empirische Verteilungsfunktion. | |||
* Bei wieviel Prozent der Turniere schied B.B. vor dem Achtelfinale aus? | |||
* Bei wieviel Prozent der Turniere erreichte B.B. mindestens das Halbfinale? | |||
* Bei wie vielen Turnieren spielte B.B. noch in der 2. Runde mit? | |||
* In welcher Runde spätestens schied B.B. bei 80% der Turniere aus? | |||
* In welcher Runde schied B.B. bei genau 40% der Turniere aus? | |||
* Interpretieren Sie – bezogen auf den Aufgabentext – kurz den Funktionswert <math>F(x)</math> an der Stelle <math>x = 7</math>. | |||
{{Loesung|Walzabteilung|65}} | |||
In einer Walzabteilung bedienen 4 Arbeiter (A, B, C und D) unterschiedlich moderne Maschinen. Sie benötigen jeweils folgende Durchschnittszeiten zum Walzen eines Stückes Blech: | |||
{| | |||
| A: 20 Sek/Stück | |||
| B: 30 Sek/Stück | |||
|- | |||
| C: 60 Sek/Stück | |||
| D: 60 Sek/Stück | |||
|} | |||
I. Betrachten Sie die Variable X: “Bearbeitungszeit in sec/Stück”. | |||
<ul> | |||
<li><p>Angenommen die Arbeiter arbeiten gleichlange, welche Durchschnittszeit pro Stück wird in der Abteilung benötigt?</p></li> | |||
<li><p>Angenommen den Arbeitern sind folgende Stückkontingente vorgegeben:</p> | |||
{| | {| | ||
| A: 1000 Stück | |||
| B: 500 Stück | |||
|- | |- | ||
| | | C: 300 Stück | ||
| | | D: 200 Stück | ||
| | |} | ||
<p>welche Durchschnittszeit pro Stück wird in der Abteilung jetzt benötigt?</p></li></ul> | |||
II. Betrachten Sie die Variable Y: “hergestellte Stück pro Stunde”. | |||
* Angenommen die Arbeiter arbeiten gleichlange, wie viel Stück werden im Durchschnitt pro Stunde gewalzt? | |||
* Angenommen den Arbeitern sind die Stückkontingente von I b) vorgegeben, wie viel Stück pro Stunde werden jetzt im Durchschnitt gewalzt? | |||
| | {{Loesung|Wanderer|66}} | ||
Ein Wanderer legte 2 Kilometer zur<span>ü</span>ck. Den ersten Kilometer ging er mit einer Geschwindigkeit von 6 km je Stunde, den zweiten mit einer Geschwindigkeit von 4 km je Stunde. | |||
Wie groß war seine Durchschnittsgeschwindigkeit? | |||
{{Loesung|WM–Berichterstattung|67}} | |||
Um festzustellen, wie viele Stunden pro Spieltag ein Fu“sball–Fan die WM–Berichterstattung im Fernsehen während der letzten Fu”sball–WM verfolgte, wurden 20 Fußball–Fans in A–Dorf nach ihrem Fernsehkonsum während der WM befragt. Die Befragung brachte folgendes Ergebnis: | |||
{| | {|class="wikitable" | ||
|align="right"| | ! Stunden | ||
|align="right"| | !align="right"| 0 | ||
!align="right"| 1 | |||
!align="right"| 2 | |||
!align="right"| 3 | |||
!align="right"| 4 | |||
|- | |- | ||
| | | relative Häufigkeit | ||
|align="right"| 0.05 | |||
|align="right"| 0.1 | |||
|align="right"| 0.4 | |||
|align="right"| 0.2 | |||
|align="right"| 0.25 | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|align="right"| | |||
|} | |} | ||
* Wie lautet das hier untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret? | |||
* Bestimmen Sie tabellarisch die absoluten und relativen Häufigkeiten und die empirische Verteilungsfunktion. | |||
* Wieviele Stunden sehen 10% der Befragten höchstens fern? | |||
* Geben sie an, wieviele Stunden 85% der Befragten mindestens fernsehen. | |||
* Geben Sie die Stundenzahl an, die genau 20% der Befragten fernsehen. | |||
{{Loesung|Zigaretten|68}} | |||
Im Rahmen einer medizinischen Untersuchung in S–Stadt im Januar wurden 200 Personen zufällig befragt, wieviele Zigaretten sie pro Tag rauchen. Das Ergebnis dieser Untersuchung sei in folgender Graphik beschrieben:<br /> | |||
[[File:Bild3.jpg|image]] | |||
* Wie heißt die obige Darstellungsform? Welche Annahmen wurden hinsichtlich der Verteilung innerhalb jeder Klasse getroffen? | |||
* Geben Sie die absoluten und relativen Klassenhäufigkeiten, die Häufigkeitsdichten und die empirische Verteilungsfunktion an. | |||
* Geben Sie an, wie hoch der Anteil der Befragten ist, die mindestens 20 Zigaretten pro Tag rauchen. | |||
| | {{Loesung|Zuckergewicht|69}} | ||
|} | |||
Das Füllgewicht von 75 maschinell abgepackten Paketen Zucker wurde kontrolliert. Die Messwerte ergeben folgende Häufigkeitsverteilung: | |||
{|class="wikitable" | |||
!align="right"| Füllgewicht (in g) | |||
!align="right"| Anzahl der Pakete | |||
{| | |||
!align="right"| | |||
!align="right"| | |||
|- | |- | ||
|align="right"| | |align="right"| 980 – 990 | ||
|align="right"| | |align="right"| 5 | ||
|align="right"| | |- | ||
|align="right"| 990 – 995 | |||
|align="right"| 12 | |||
|- | |||
|align="right"| 995 – 1000 | |||
|align="right"| 23 | |||
|- | |||
|align="right"| 1000 – 1005 | |||
|align="right"| 22 | |||
|- | |- | ||
|align="right"| | |align="right"| 1005 – 1010 | ||
|align="right"| | |align="right"| 11 | ||
|- | |- | ||
|align="right"| | |align="right"| 1010 – 1020 | ||
|align="right"| | |align="right"| 2 | ||
|} | |} | ||
Berechnen Sie den Modus, den Median und das arithmetische Mittel des Füllgewichts. | |||
{{Loesung|Zugfolge - Teil I|70}} | |||
1. | An einer Schranke der Bahnstrecke von A nach B wurden am 20.1.folgende Abstände der Zugfolge in Minuten gemessen:<br /> | ||
<br /> | |||
59; 43; 36; 63; 23; 4; 29; 41; 43; 31; 29; 69; 57; 36; 112; 43; 14; 11; 18; 77; 81; 47; 12; 43; 44; 16; 80; 6; 52; 5; 5; 6; 21; 43; 44; 46; 51 | |||
4 | |||
5 | |||
6 | |||
* Wie ist das Erhebungsmerkmal skaliert? Ist es häufbar, nicht häufbar, stetig, diskret? | |||
* Ermitteln Sie die absolute und relative Klassenhäufigkeiten unter Verwendung von Klassen der Breite 30 Minuten. Stellen Sie die Häufigkeitsverteilung graphisch dar. | |||
* Geben Sie die empirische Verteilungsfunktion an und stellen Sie diese graphisch dar. | |||
* Wie | |||
* | |||
* | |||
{| | {{Loesung|Zugfolge - Teil II|71}} | ||
* | * Berechnen Sie aufgrund der Häufigkeitsverteilung der klassierten Daten für das Erhebungsmerkmal <math>X</math>: “Zugfolgeabstand” der Aufgabe [[Univariate Statistik/Aufgaben#Zugfolge - Teil II|davor]] drei aussagekräftige Lageparameter. | ||
* Welcher durchschnittlicher Zugfolgeabstand ergibt sich auf der Basis der Urliste? Wie erklären Sie sich den Unterschied zum zahlenmäßigen Ergebnis des gleichen Mittelwertes aus Frage a)? | |||
* | |||
Aktuelle Version vom 15. Juli 2019, 08:05 Uhr
Anstieg der Produktion
(Lösung)
Im Unternehmen U stieg die Produktion des Erzeugnisses E von 2005 bis 2007 im Mittel jährlich um 10%, von 2007 bis 2009 im Mittel jährlich um 20%.
- Wie hoch war das mittlere Entwicklungstempo der E–Produktion im Unternehmen U von 2005 bis 2009?
- Auf wieviel Prozent würde die E–Produktion 2011 gegenüber 2007 bei Fortsetzung des mittleren Entwicklungstempos von 2007 bis 2009 steigen?
Arbeitslose
(Lösung)
Ein Bundesland ist in zwei Arbeitsamtsbezirke eingeteilt. In diesen werden für einen bestimmten Monat folgende Anteile der Arbeitslosen an den Erwerbspersonen (Arbeitslosenquote) und Arbeitslosenzahlen ermittelt:
| Bezirk–Nr. | 1 | 2 |
|---|---|---|
| Arbeitslosenquote | 5% | 20% |
| Arbeitslosenzahl | 3000 | 4000 |
Bestimmen sie die Arbeitslosenquote für dieses Bundesland.
Auswirkung der Regelstudienzeit
(Lösung)
Um die Auswirkung der Regelstudienzeit zu demonstrieren, wurden im Januar die Studienzeiten von 200 Wirtschaftsingenieuren in der Bundesrepublik Deutschland erhoben, die in den vergangenen 4 Semestern ihr Studium abgeschlossen haben. Es ergaben sich folgende Daten (fiktive Daten):
| Semesterzahl | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|
| relative Häufigkeit | 0,1 | 0,1 | 0,4 | 0,2 | 0,15 | 0,05 |
- Wie heißt das untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret?
- Bestimmen Sie die absoluten und relativen Häufigkeiten.
- Bestimmen Sie die empirische Verteilungsfunktion.
- Wie viele Semester höchstens benötigten die 10% schnellsten Studenten?
- Wie viele Semester mindestens benötigten die 80% langsamsten Studenten?
- Geben Sie die Semesterzahl an, die genau 20% der Studenten benötigten.
Von nun an soll nur noch das Merkmal : “Semesterzahl” mit den Ausprägungen
- “klein” (weniger als 12 Semester)
- “mittel” (genau 12 Semester)
- “groß” (mehr als 12 Semester)
betrachtet werden.
- Welche Skalierungsart liegt jetzt vor?
- Zeichnen Sie die Häufigkeitsverteilung.
- Ist es sinnvoll, bei einem nominalskalierten Merkmal eine Verteilungsfunktion anzugeben? Begründen Sie Ihre Antwort.
Benzinverbrauch
(Lösung)
Bei einer Testreihe, die den Benzinverbrauch eines Autotyps in Deutschland erfasste, erhielt man folgende Daten:
- arithmetisches Mittel: 8,2 [Liter/100km]
- Standardabweichung: 0,41 [Liter/100km]
Für den Export in die USA müssen die Verbrauchsdaten in Gallonen/100 Meilen angegeben werden (1 Gallone = 3,785 Liter, 1 Meile = 1,609km) Welchen Wert hat der Variationskoeffizient v, wenn der Benzinverbrauch in Gallonen/100 Meilen ausgewiesen wird?
Berliner Luftqualität
(Lösung)
An einer Messstation zur Kontrolle des Stickstoffmonoxydgehalts in der Berliner Luft wurden im März an 15 Tagen die folgenden Werte ermittelt ():
| 35; | 36; | 37; | 27; | 43; |
| 23; | 33; | 31; | 21; | 35; |
| 26; | 38; | 34; | 33; | 28; |
- Wie lautet das untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret?
- Fassen Sie die Messwerte in folgende Klassen zusammen:
19,5–29,5;29,5–34,5;34,5–39,5;39,5–44,5
- Zeichnen Sie für die klassierten Daten die Häufigkeitsverteilung und die empirische Verteilungsfunktion.
- An wieviel Tagen betrug der Stickstoffmonoxydgehalt der Luft mindestens 34,5 ?
- Wieviel Stickstoffmonoxydgehalt war an den 80% “saubersten” Tagen höchstens in der Luft?
Besuche pro Woche
(Lösung)
50 Studenten wurden danach gefragt, wie oft sie in der vergangenen Woche ihre Freundin besucht haben. Das Ergebnis ist folgendes:
| 0; | 3; | 2; | 6; | 4; | 0; | 0; | 1; | 4; | 3; |
| 1; | 1; | 1; | 7; | 1; | 6; | 0; | 2; | 7; | 1; |
| 0; | 7; | 0; | 5; | 1; | 2; | 1; | 6; | 4; | 1; |
| 5; | 9; | 4; | 0; | 3; | 6; | 4; | 3; | 2; | 5; |
| 4; | 3; | 2; | 1; | 4; | 1; | 3; | 5; | 3; | 6; |
- Erstellen Sie die absolute und relative Häufigkeitsverteilung und die empirische Verteilungsfunktion.
- Wie oft besuchte ein Student durchschnittlich seine Freundin?
Bevölkerungsdichte und Ärztedichte
(Lösung)
Für die drei Regionen eines Landes sind jeweils die Bevölkerungsdichte X (Einwohner je km) und die Ärztedichte Y (Ärzte je 1 000 Einwohner) gegeben:
| Region | Fläche (in km) | Bevölkerungs- | Ärzte- | Ärzte- |
| dichte | zahl | dichte | ||
| 1 | 10 000 | 60 | 300 | 0,50 |
| 2 | 6 000 | 200 | 1 200 | 1,00 |
| 3 | 4 000 | 300 | 1 500 | 1,25 |
Berechnen Sie die Bevölkerungsdichte X und die Ärztedichte Y für das gesamte Land.
Bibliotheken - Teil I
(Lösung)
Aus der Erhebung “Deutsche Bibliotheksstatistik ”, Berlin , wurden für die zentralen Universitätsbibliotheken nachstehende Angaben über die Öffnungszeiten (Std./Wo.), die Ausleihzeiten (Std./Wo), den Etat für Neuerwerb (Mrd. EUR/Jahr) und die Planstellen entnommen:
| Universitätsbibliothek | Öffnungszeiten | Ausleihzeiten | Etat für Neuerwerb | Planstellen |
|---|---|---|---|---|
| RWTH Aachen | 66 | 30 | 3.31 | 106 |
| Augsburg | 75 | 75 | 4.03 | 101 |
| Bamberg | 59 | 48 | 4.69 | 72 |
| Bayreuth | 64 | 64 | 5.77 | 72 |
| HU Berlin | 53 | 53 | 5.86 | 205 |
| FU Berlin | 59 | 41 | 4.22 | 146 |
| TU Berlin | 69 | 42 | 5.86 | 181 |
| Bielefeld | 111 | 98 | 4.44 | 166 |
| Bochum | 59 | 59 | 2.73 | 97 |
| Bonn | 63 | 54 | 3.26 | 153 |
| TU Braunschweig | 50 | 50 | 2.28 | 74 |
| UB Bremen | 59 | 52 | 5.59 | 150 |
| Chemnitz | 56 | 44 | 1.43 | 89 |
| Clausthal-Zellerfeld | 43 | 29 | 1.05 | 32 |
| TH Darmstadt | 54 | 26 | 2.25 | 91 |
| Dortmund | 53 | 53 | 4.35 | 143 |
| TU Dresden | 59 | 59 | 3.00 | 180 |
| Düsseldorf | 59 | 59 | 5.97 | 161 |
| Duisburg | 68 | 49 | 3.43 | 74 |
| KU Eichstätt | 64 | 43 | 4.67 | 78 |
| Erlangen-Nürnberg | 64 | 45 | 2.51 | 157 |
| Essen | 65 | 65 | 4.44 | 84 |
| Frankfurt (SB) | 61 | 40 | 1.58 | 35 |
| Frankfurt (UB) | 69 | 40 | 2.76 | 187 |
| Freiburg | 64 | 43 | 3.83 | 119 |
| Gießen | 59 | 45 | 1.71 | 77 |
| Greifswald | 74 | 36 | 1.32 | 100 |
| Göttingen | 60 | 34 | 6.56 | 260 |
| Halle | 79 | 45 | 1.80 | 154 |
| Hamburg | 63 | 41 | 4.05 | 211 |
| Hannover | 48 | 36 | 1.79 | 83 |
| Heidelberg | 83 | 39 | 4.24 | 119 |
| Jena | 62 | 32 | 3.00 | 158 |
| Kaiserslautern | 50 | 50 | 2.50 | 61 |
| Karlsruhe | 54 | 54 | 2.58 | 77 |
| GHS Kassel | 64 | 49 | 3.87 | 111 |
| Kiel | 67 | 37 | 2.87 | 100 |
| Konstanz | 89 | 87 | 5.51 | 116 |
| Köln | 62 | 33 | 3.85 | 146 |
| Leipzig | 72 | 45 | 2.20 | 179 |
| TU Magdeburg | 51 | 51 | 1.52 | 53 |
| Mainz | 58 | 48 | 1.67 | 108 |
| Mannheim | 63 | 33 | 1.50 | 90 |
| Marburg | 84 | 28 | 1.60 | 120 |
| LMU München | 60 | 45 | 1.63 | 107 |
| TU München | 52 | 37 | 2.95 | 99 |
| Münster | 69 | 38 | 3.67 | 145 |
| Oldenburg | 65 | 60 | 3.60 | 99 |
| Osnabrück | 57 | 43 | 4.74 | 99 |
| Paderborn | 86 | 86 | 3.60 | 75 |
| Passau | 74 | 41 | 4.96 | 70 |
| Regensburg | 74 | 36 | 4.25 | 191 |
| Rostock | 56 | 53 | 3.28 | 129 |
| Saarbrücken | 64 | 28 | 3.00 | 101 |
| Siegen | 75 | 71 | 3.30 | 73 |
| Stuttgart | 62 | 34 | 0.85 | 78 |
| Stuttgart-Hohenheim | 79 | 76 | 1.74 | 41 |
| Trier | 73 | 29 | 3.76 | 97 |
| Tübingen | 70 | 38 | 4.14 | 139 |
| Ulm | 64 | 64 | 3.07 | 66 |
| Würzburg | 64 | 64 | 1.49 | 122 |
| Wuppertal | 71 | 60 | 3.74 | 74 |
Wie sind die Erhebungsmerkmale skaliert? Sind sie häufbar, nicht häufbar, stetig, diskret (quasi-stetig)?
Ermitteln Sie unter Verwendung nachstehender Klassen (von ... bis unter...)
“Öffnungszeiten” 40-50, 50–60, 60–70, 70–80, 80–90, 90–115
“Ausleihzeiten” 25–30, 30–40, 40–50, 50–60, 60–70, 70–80, 80–100
“Etat für Neuerwerb” 0–1, 1–2, 2–3, 3–4, 4–5, 5–6, 6–7
“Planstellen” 30–70, 70–80, 80–100, 100–150, 150–200, 200–270
die absoluten und relativen Klassenhäufigkeiten sowie die empirische Verteilungsfunktion.
Stellen Sie die Häufigkeitsverteilungen und die empirische Verteilungsfunktion graphisch dar.
Berechnen Sie ausgehend von den unter b) erstellten empirischen Verteilungsfunktionen:
Welcher Anteil der Universitätsbibliotheken hatte eine Öffnungszeit zwischen 48 und 74 Std./Wo.?
Welcher Anteil der Universitätsbibliotheken hatte eine Ausleihzeit über 65 Std./Wo.?
Welcher Anteil der Universitätsbibliotheken hatte einen Etat für Neuerwerb von höchstens 2,4 Mrd. EUR/Jahr?
Welcher Anteil der Universitätsbibliotheken hatte mehr als 100 Planstellen?
Wieviele Planstellen höchstens hatten die 25% personell am schwächsten besetzten Universitätsbibliotheken?
Wie lange waren die 15% leserfreundlichsten Universitätsbibliotheken mindestens geöffnet?
Bibliotheken - Teil II
(Lösung)
Die folgenden Fragen beziehen sich auf die Häufigkeitsverteilungen der klassierten Daten der [Aufgabe12].
- Berechnen Sie drei aussagekräftige Mittelwerte für das Erhebungsmerkmal : “Öffnungszeiten”.
- Ermitteln Sie ebenfalls drei sinnvolle Mittelwerte für das Erhebungsmerkmal : “Ausleihzeiten”.
- Ist der Modus ein aussagekräftiger Mittelwert für das Erhebungsmerkmal : “Etat für Neuerwerb”?
- Berechnen Sie für das Merkmal : “Etat für Neuerwerb” die Quartile. Zeichnen Sie einen Boxplot.
Bibliotheken - Teil III
(Lösung)
In [Aufgabe12] wurden für die zentralen Universitätsbibliotheken der Bundesrepublik Deutschland unter anderem die beiden Merkmale : “Öffnungszeiten” und : “Ausleihzeiten” untersucht. Beantworten Sie ausgehend von den Häufigkeitsverteilungen der klassierten Daten der Merkmale folgende Frage:
Welches der beiden Merkmale weist die größere Streuung auf Basis der Standardabweichung auf? (Runden Sie für Ihre Berechnungen den zugrundegelegten Mittelwert auf eine Stelle nach dem Komma.)
Brutto- und Nettoeinkommen
(Lösung)
Das Bruttoeinkommen aus unselbständiger Arbeit je Beschäftigten und Monat in der Bundesrepublik Deutschland stieg von 3 012 DM im Jahre 1980 auf 4 112 DM im Jahre 1989. Die Nettolohn– und –gehaltssumme je Beschäftigten und Monat veränderte sich von 1 765 DM im Jahre 1980 auf 2 261 DM im Jahre 1989.
Quelle: Zahlen zur wirtschaftlichen Entwicklung der Bundesrepublik
Deutschland 1991, Institut der Deutschen Wirtschaft Köln, S. 30.
Vergleichen Sie das Bruttoeinkommen und das Nettoeinkommen je Beschäftigten bezüglich ihres mittleren Entwicklungstempo im Zeitraum 1980–1989.
CDs
(Lösung)
In der Umsatzstatistik eines Einzelhändlers für das zurückliegende Geschäftsjahr sind für die drei Sorten CDs folgende Preise und Umsätze ausgewiesen:
| Sorte | 1 | 2 | 3 |
|---|---|---|---|
| Preis | 3,90 | 4,50 | 4,90 |
| Umsatz | 1224,60 | 967,50 | 519,40 |
- Berechnen Sie den Durchschnittspreis für CDs im vergangenen Geschäftsjahr.
- Berechnen Sie die Standardabweichung des Preises für CDs.
Das erste Tor
(Lösung)
Der folgenden Liste ist zu entnehmen, wieviele Minuten man bei jedem von 25 Fußballspielen warten musste, bis das erste Tor fiel:
| 40; | 65; | 11; | 43; | 34; | 41; | 3; | 1; | 43; | 9; |
| 21; | 4; | 12; | 41; | 9; | 46; | 14; | 29; | 41; | 7; |
| 31; | 43; | 25; | 23; | 16 |
Auf der Grundlage einer Gruppierung mit vier Klassen (1. Klasse: 0 - 15, 2. Klasse: 15 - 30, 3. Klasse: 30 - 45, 4. Klasse: 45 - 90min) beantworten Sie die Frage zu: Wie groß ist der Anteil der Spiele, bei denen man mehr als 20, aber höchstens 60 Minuten auf das erste Tor warten musste?
Ladekabel
(Lösung)
In den Städten A, B und C wurden jeweils in mehreren Geschäften die Preise für einen bestimmtes Ladekabel ermittelt. Im Ort A ergab sich aufgrund von 11 Einzelwerten ein Durchschnittspreis von 16,44 EUR. In B betrug der Durchschnittspreis basierend auf 6 Einzelwerten 15,28 EUR und in C wurde nach dem Besuch von 13 Geschäften als Durchschnittspreis 14,86 EUR ermittelt.
Wie hoch ist der Durchschnittspreis des Ladekabels unter Berücksichtigung sämtlicher Preisinformationen aus den Städten A, B und C?
Drei Betriebe
(Lösung)
Für die 3 Betriebe eines Unternehmens liegen folgende Angaben vor (TEUR = 1000 EUR):
| Betrieb | Materialverbrauch | Produktion | Materialverbrauch |
| in EUR je TEUR | in TEUR | in TEUR | |
| Produktion 2010 | 2010 | 2011 | |
| 1 | 750 | 80 400 | 55 800 |
| 2 | 800 | 26 600 | 18 350 |
| 3 | 700 | 60 000 | 45 850 |
Der Materialverbrauch des Unternehmens betrug im Jahre 2007: 135 548 TEUR.
- Ermitteln Sie den durchschnittlichen Materialverbrauch je TEUR Produktion des Unternehmens für das Jahr 2010.
- Geben Sie das untersuchte statistische Merkmal an. Wie ist es skaliert?
- Wie hoch wird voraussichtlich der Materialverbrauch des Unternehmens im Jahre 2013 sein, wenn das mittlere jährliche Entwicklungstempo des Zeitraumes 2007 – 2011 weiterhin beibehalten wird?
Drei Stichproben
(Lösung)
Von drei verschiedenen Stichproben mit nur positiven Beobachtungswerten sind folgende Informationen gegeben:
| Stichprobe | 1 | 2 | 3 |
|---|---|---|---|
| Stichprobenumfang | 10 | 40 | 50 |
| arithmetisches Mittel | 51 | 53 | 54 |
| Varianz | 21 | 22 | 23 |
Die drei Stichproben werden zu einer einzigen Stichprobe vereinigt. Berechnen Sie die Varianz für die gesamte Stichprobe.
Eine Befragung von Studierenden - Teil I
(Lösung)
Für eine Untersuchung von Studierenden an einer deutschen Hochschule wurden im Juni 25 Studierende nach dem Studiengang, der Anzahl der Geschwister und nach dem Einkommen befragt. Das Ergebnis war:
| Name | Studiengang | Zahl der | Einkommen | |
| Geschwister | ||||
| 1 | Martin A. | VWL | 0 | 924 |
| 2 | Ute A. | Sozialwiss. | 1 | 789 |
| 3 | Wilhelm A. | BWL | 0 | 1 365 |
| 4 | Kurt B. | BWL | 1 | 683 |
| 5 | Sylvia B. | Polit.Wiss. | 1 | 744 |
| 6 | Elke D. | Polit.Wiss. | 2 | 640 |
| 7 | Klaus D. | Sozialwiss. | 2 | 631 |
| 8 | Theo E. | VWL | 1 | 814 |
| 9 | Jean F. | Polit.Wiss. | 1 | 778 |
| 10 | Elvira G. | BWL | 0 | 1 062 |
| 11 | Karl H. | BWL | 0 | 1 230 |
| 12 | Andreas K. | VWL | 1 | 700 |
| 13 | Thomas K. | BWL | 0 | 850 |
| 14 | Chris L. | Sozialwiss. | 3 | 641 |
| 15 | Uwe L. | Polit.Wiss. | 2 | 640 |
| 16 | Axel M. | BWL | 0 | 850 |
| 17 | Maria M. | BWL | 1 | 683 |
| 18 | Ruth M. | Sozialwiss. | 0 | 616 |
| 19 | Bärbel N. | BWL | 1 | 683 |
| 20 | Armin R. | BWL | 2 | 683 |
| 21 | Christa R. | VWL | 1 | 660 |
| 22 | Bernd S. | BWL | 1 | 1 440 |
| 23 | Claudia S. | Sozialwiss. | 3 | 794 |
| 24 | Erich T. | VWL | 0 | 660 |
| 25 | Claudia W. | Polit.Wiss. | 1 | 640 |
- Was ist bei dieser Befragung die Grundgesamtheit, was sind die einzelnen statistischen Einheiten? Durch welche Identifikationskriterien ist die untersuchte Grundgesamtheit festgelegt?
- Wie ist das Erhebungsmerkmal “Studiengang” skaliert? Ermitteln Sie aus der obigen Urliste die absolute und relative Häufigkeitsverteilung für dieses Merkmal. Stellen Sie die Häufigkeitsverteilung graphisch dar.
- Wie ist das Erhebungsmerkmal “Anzahl der Geschwister” skaliert? Ermitteln Sie die absolute und relative Häufigkeitsverteilung für dieses Merkmal. Erstellen Sie die empirische Verteilungsfunktion. Stellen Sie die Häufigkeitsverteilung und die empirische Verteilungsfunktion graphisch dar.
- Wie viele Studierende haben höchstens 2 Geschwister? Wie viel Prozent der Studierenden haben mindestens 2 Geschwister? Wie viel Prozent der Studierenden haben ein oder zwei Geschwister?
- Wie ist das Erhebungsmerkmal “Einkommen” skaliert? Ermitteln Sie die absolute und relative Häufigkeitsverteilung für dieses Merkmal unter Verwendung folgender Einkommensklassen (von ... bis unter ...): 600–650, 650–700, 700–900, 900–1200, 1200–1450. Erstellen Sie die empirische Verteilungsfunktion. Stellen Sie die Häufigkeitsverteilung und die empirische Verteilungsfunktion graphisch dar.
- Berechnen Sie ausgehend von der Einkommensverteilung unter e):
- Welcher Anteil der Studierenden hat ein Einkommen von mindestens 750 und höchstens 1300 EUR?
- Welcher Anteil der Studierenden hat ein Einkommen von mehr als 800 EUR?
- Welches Einkommen hatten die 50% einkommensschwächsten Studierenden höchstens?
- Welches Einkommen hatten die 20% einkommensstärksten Studierenden mindestens?
Eine Befragung von Studierenden - Teil II
(Lösung)
Bezogen auf die Aufgabe davor.
- Ermitteln Sie einen geeigneten Lageparameter für das Erhebungsmerkmal : “Studiengang”.
- Ermitteln Sie drei geeignete Lageparameter für das Erhebungsmerkmal : “Anzahl der Geschwister”.
- Berechnen Sie basierend auf der Urliste das durchschnittliche Einkommen eines/einer Studierenden.
- Berechnen Sie basierend auf der Häufigkeitsverteilung der klassierten Daten des Erhebungsmerkmals : “Einkommen” zwei aussagekräftige Lageparameter, die Quartile und das 90%–Quantil.
- Geben Sie für das Merkmal “Einkommen” die 5 - Zahlen - Zusammenfassung (Min, Max, Median, unteres und oberes Quartil) an und zeichnen Sie den Box–Plot.
Einkommen der Beamten
(Lösung)
In der Auswertung einer statistischen Erhebung vom April 2012 erhielt die Hälfte der befragten Beamten in einer Region ein monatliches Nettoeinkommen unter 2590 EUR. 1/4 der Beamten erhielten mehr als 3590 EUR. Während die gesamte Einkommensspannweite mit 8000 EUR angegeben wird, wird für die mittleren 50% der Beamten eine Einkommensspannweite von 1770 EUR ausgewiesen. Das geringste Einkommen lag bei 500 EUR. Die Standardabweichung der Nettoeinkommen wird mit 1620 EUR angegeben. Das sind 54% des durchschnittlichen Nettoeinkommens.
Bestimmen Sie das 25%–Quartil des Nettoeinkommens der befragten Beamten.
Einkommensgleichheit
(Lösung)
Ein Ökonom möchte die relative Einkommensgleichheit auf den drei melanesischen Inseln Atoll A, B und C vergleichen. Auf jeder Insel leben 8 Personen. Zahlungsmittel auf den Inseln sind Kauri Schnecken. Als geeignetes Maß erscheint dem Ökonomen der Variationskoeffizient. Berechnen Sie diesen für Atoll A mit folgender Einkommenstabelle.
| Atoll A Einkommen | |
| Person | in Kauri Schnecken |
| 1 | 225 |
| 2 | 185 |
| 3 | 250 |
| 4 | 150 |
| 5 | 237 |
| 6 | 100 |
| 7 | 87 |
| 8 | 305 |
Einkommen und Alter
(Lösung)
50 Personen wurden nach dem Einkommen (EUR) und dem Alter (Jahre) befragt. Im Ergebnis ergab sich nachstehende Korrelationstabelle:
| Einkommen | |||||
| 20–30 | 30–40 | 40–50 | 50–60 | 60–70 | |
| 0–1000 | 1 | 2 | 1 | 1 | 1 |
| 1000–1500 | 2 | 4 | 4 | 3 | 1 |
| 1500–2000 | 3 | 6 | 6 | 3 | 2 |
| 2000–3000 | 1 | 3 | 2 | 2 | 2 |
- Erstellen Sie die Korrelationstabelle mit den relativen Häufigkeiten.
- Bestimmen Sie die Randverteilungen.
- Bestimmen Sie für jede Altersgruppe die bedingte Verteilung des Einkommens.
- Bestimmen Sie für jede Einkommensgruppe die bedingte Verteilung des Alters.
- Berechnen Sie das durchschnittliche Einkommen der 50 Personen.
- Berechnen Sie das durchschnittliche Alter der 50 Personen.
- Bestimmen Sie das am häufigsten aufgetretene Einkommen.
- Welches Einkommen höchstens hatten die 50% ärmsten Personen?
- Berechnen Sie die durchschnittlichen bedingten Einkommen je Altersgruppe.
- Berechnen Sie die Standardabweichung des Einkommens.
- Berechnen Sie die Kovarianz zwischen Einkommen und Alter.
Einwohnerzahlen
(Lösung)
Für das Jahr 1980 wurden nachstehende Einwohnerzahlen (in Millionen) im Fischer–Weltalmanach 2000 veröffentlicht.
| Land | Einwohner | Land | Einwohner |
| (Millionen) | (Millionen) | ||
| Bangladesh | 87 | Indonesien | 148 |
| Brasilien | 122 | Japan | 117 |
| China | 981 | Pakistan | 83 |
| Deutschland | 78 | Russland | 139 |
| Indien | 687 | USA | 227 |
Berechnen Sie einen aussagekräftigen Mittelwert.
Eiskugelkonsum
(Lösung)
Der Eisverkäufer Hardy möchte seinen Kunden täglich frisches Eis verkaufen. Damit er immer die richtigen Mengen vorrätig hat und in Zukunft besser planen kann, zählt er an einem Tag bei 200 Kunden den Eiskugelkonsum:
Kein Kunde hat genau 2 oder mehr als 6 Kugeln verlangt. Je 20% der Kunden wollten 1 Kugel oder mindestens 5 Kugeln. Höchstens 3 Kugeln verlangten 45% der Kunden. Die Summe der Anteile der Kunden, die 4 bzw. 6 Kugeln wollten, war zehnmal so hoch wie der Anteil der Kunden, die 5 Kugeln verlangten.
- Wie lautet das untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret?
- Bestimmen sie tabellarisch die absoluten und relativen Häufigkeiten sowie die empirische Verteilungsfunktion.
- Stellen Sie die Häufigkeitsverteilung und die empirische Verteilungsfunktion graphisch dar.
- Wie viel Prozent der Kunden kauften höchstens 5 Kugeln Eis?
- Wie viele Kugeln Eis mindestens kauften 80% der Kunden?
- Wie viele Kugeln Eis kauften genau 35% der Kunden?
Erdbeerplantage - Teil I
(Lösung)
Der Student Alois besitzt eine Erdbeerplantage in Bayern, um sich damit sein Studium zu finanzieren. Da das Ernteergebnis je nach “Qualität des Sommers” verschieden ist, notierte sich Alois, wie viele Stunden die Sonne in der diesjährigen Saison pro Tag auf seine Beeren einwirkte:
| Sonnenstunden pro Tag | |
| von ... bis unter ... | Anzahl der Tage |
| 0 – 2 | 20 |
| 2 – 3 | 15 |
| 3 – 5 | 20 |
| 5 – 8 | 35 |
| 8 – 12 | 10 |
Mit der Auswertung der Daten erhofft er sich Aufschlüsse über den zu erwartenden Ertrag seiner Plantage.
- Wie lautet das untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret?
- Stellen Sie die Häufigkeiten aus der Tabelle graphisch dar.
- Zeichnen Sie die empirische Verteilungsfunktion.
- An wie vielen Tagen der Saison schien die Sonne mindestens 4 Stunden?
- Wie lange höchstens schien die Sonne an den 40 sonnenärmsten Tagen der Saison?
- An wie vielen Tagen in dieser Saison schien die Sonne prozentual 4 und 9 Stunden?
Erdbeerplantage - Teil II
(Lösung)
Der Student Alois, aus der Aufgabe davor, möchte wissen:
- Wie viele Stunden schien die Sonne durchschnittlich pro Tag in der Saison?
- Wie lange schien die Sonne höchstens an den 50% sonnenärmsten Tagen der Saison?
Festgeldkonten
(Lösung)
Eine internationale Bank, die in 5 Ländern agiert, bietet Festgeldkonten an. Die Einlagen werden länderabhängig mit einem variablen Zinssatz verzinst, wobei der länderspezifische, variable Zinssatz, ein länderunabhängiger Zinsatz und der Median der Zinssätze für Einlagen im jeweiligen Land sind. Der länderunabhängige Zinssatz beträgt . Die länderspezifischen Verteilungen der Einlagezinssätze sind in nachfolgender Tabelle gegeben:
| Zinssätze | Land 1 | Land 2 | Land 3 | Land 4 | Land 5 |
|---|---|---|---|---|---|
| 4,0 – 4,5% | 0,200 | 0,050 | 0,020 | 0,150 | 0,275 |
| 4,5 – 5,0% | 0,240 | 0,110 | 0,055 | 0,350 | 0,375 |
| 5,0 – 5,5% | 0,300 | 0,340 | 0,300 | 0,350 | 0,350 |
| 5,5 – 6,0% | 0,260 | 0,500 | 0,625 | 0,150 | 0,000 |
Berechnen Sie den durchschnittlichen variablen Zinssatz für Festgeldkonten dieser internationalen Bank.
Fließband
(Lösung)
An einem Fließband sind 6 Arbeiter acht Stunden am Tag mit der Kontrolle eines elektronischen Bauteils beschäftigt. Um ein Bauteil zu kontrollieren, benötigen sie folgende Zeiten:
| Arbeiter | Stückzeit (in Minuten) |
|---|---|
| A | 2 |
| B | 4 |
| C | 8 |
| D | 10 |
| E | 8 |
| F | 5 |
Berechnen Sie einen geeigneten Mittelwert für die Kontrollzeit pro Stück an diesem Fließband.
Führerschein–Entziehungen
(Lösung)
Promille gefährden den Führerschein!
Bei den im Jahre 1990 durchgeführten Kontrollen wurde für die angegebenen Altersklassen nachstehende Anzahlen von Führerschein–Entziehungen registriert.
nach: Berliner Zeitung vom 29.2./1.3.1992
| Alter (Jahre) | Führerschein–Entziehungen |
|---|---|
| 20 – 30 | 40 500 |
| 30 – 40 | 29 200 |
| 40 – 50 | 22 100 |
| 50 – 60 | 12 600 |
- Berechnen Sie das Durchschnittsalter der betroffenen Fahrer(innen).
- Berechnen Sie die Standardabweichung des Alters und den Variationskoeffizienten (runden Sie dafür das Durchschnittsalter auf ganze Jahre auf bzw. ab).
- In welchem Altersbereich liegen die mittleren 50% der betroffenen Fahrer(innen)?
- Welches Alter höchstens hatten die 50% jüngsten Fahrer(innen) mit Führerschein–Entzug? Welche Maßzahl haben Sie berechnet?
- Berechnen Sie zu der Ma“szahl unter d) ein geeignetes Streuungsma”s.
Gartenzwerg–Großhandel
(Lösung)
Herr Meier besitzt einen Gartenzwerg–Großhandel mit drei Filialen: Berlin, New York und Flensburg. Am Ende des Geschäftsjahres möchte er einen Überblick über die Geschäftslage erhalten und fordert deshalb in allen drei Filialen Informationen über die innerhalb des letzten Jahres eingegangenen Aufträge an.
Seine Berliner Filiale übermittelt ihm folgende Informationen:
Auftragshöhe in EUR von...bis unter... Anzahl der Aufträge 0 – 20 000 15 20 000 – 50 000 30 50 000 – 150 000 45 150 000 – 300 000 10 Wie heißt das untersuchte statistische Merkmal und wie ist es skaliert?
An welchen statistischen Einheiten wurde dieses Merkmal erhoben?
Berechnen Sie die durchschnittliche Auftragshöhe.
Die New Yorker Filiale antwortet auf Herrn Meiers Anfrage kurz und bündig: : “Auftragshöhe [in $] pro Auftrag”; 95 Aufträge; .
Um besser vergleichen zu können, möchte Herr Meier diese Angaben in EUR kennen. Berechnen Sie die durchschnittliche Auftragshöhe, wenn folgender Dollarkurs gilt: 1 $ = 1,5 EUR.Aus Flensburg erhält Herr Meier folgende Daten:
2 000 EUR; 12 000 EUR; 17 000 EUR; 12 000 EUR; 200 000 EUR.Welche(n) Mittelwert(e) können Sie in diesem Fall sinnvoll angeben? Begründen Sie für jeden die Vor– und Nachteile in Situation !
Ein Fernschreiben korrigiert die Höhe des letzten Auftrages auf 2 000 EUR. Berechnen Sie aus den korrigierten Daten die durchschnittliche Auftragshöhe.
Berechnen Sie die durchschnittliche Auftragshöhe für das gesamte Unternehmen.
Gefahrene Strecke
(Lösung)
Bei 20 Vertretern eines Versicherungsunternehmens verteilt sich die in einer Woche mit dem Firmenwagen gefahrene Strecke wie folgt:
| Gefahrene Strecke in km | Anzahl Vertreter |
|---|---|
| 0-50 | 3 |
| 50-100 | 5 |
| 100-300 | 6 |
| 300-500 | 4 |
| 500-1000 | 2 |
Geben Sie die Länge des Bereiches an, in dem die 50% der Vertreter mit den mittleren gefahrenen Streckenlängen liegen.
Gleisbaubetrieb
(Lösung)
Der Direktor eines Gleisbaubetriebes erhält folgende Information:
In der letzten Schicht von 8 Stunden haben die drei Bauzüge des Betriebes beim Verlegen von Gleisen im Mittel 180,6 Minuten pro Gleis benötigt, wobei Bauzug A 250 Minuten/Gleis, Bauzug B 166,7 Minuten/Gleis und Bauzug C 125 Minuten/Gleis brauchte.
Überprüfen Sie den angegebenen Mittelwert und korrigieren Sie ihn gegebenenfalls mit einer exakten Begründung.
Glücksspielautomaten
(Lösung)
In der Lieblingskneipe der Studentin Fritzi stehen zwei Glücksspielautomaten. Beide Automaten erwarten den gleichen Einsatz pro Spiel. Um ihre Gewinnchancen zu optimieren, spielt Fritzi mit jedem der Automaten für eine Weile. Folgende Gewinne erzielt sie in den einzelnen Spielen:
Automat A:0,01,52,01,52,02,55,51,0
Automat B:6 mal 0,5; 5 mal 1,0; 1 mal 7,5; 2 mal 5,5
Welchen Median hat der Automat mit dem größten durchschnittlichen Gewinn?
Grafische Darstellung
(Lösung)
Gegeben sind folgende Daten des statistischen Bundesamtes von 1998 über das Alter der im Straßenverkehr Getöteten innerhalb von Ortschaften.
| Alter | unter 15 | 15 - 18 | 18 - 25 | 25 - 65 | 65 - 90 |
|---|---|---|---|---|---|
| Anzahl | 126 | 76 | 258 | 808 | 638 |
Welche der folgenden grafischen Darstellungen beschreibt die Häufigkeitsverteilung der Daten korrekt?
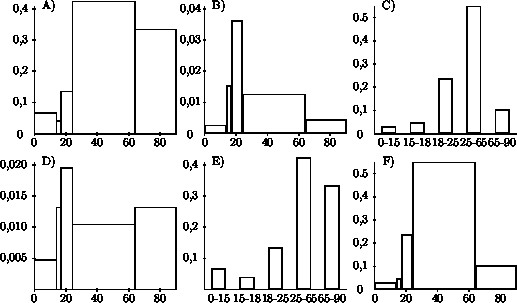
Intercity – Zug
(Lösung)
Ein Intercity – Zug legt 300 km in vier Abschnitten zurück, wobei die Geschwindigkeit wegen unterschiedlicher Streckenbeschaffenheit jeweils verschieden ist:
| Streckenabschnitt | Streckenlänge | Geschwindigkeit |
| (in km) | (in km/h) | |
| A | 100 | 150 |
| B | 60 | 120 |
| C | 50 | 100 |
| D | 90 | 90 |
Berechnen Sie die Durchschnittsgeschwindigkeit für die Gesamtstrecke.
Internetstunden
(Lösung)
Das folgende Histogramm gibt die Häufigkeitsverteilung von Internetstunden pro Woche für eine Grundgesamtheit von 100 Informatikstudenten an.
Bestimmen Sie den Median aus diesen Daten.
Kaltmieten
(Lösung)
In einem Wohnviertel mit Häusern verschiedener Wohnungseigentümer sollen die Kaltmieten analysiert werden. Aus einer ersten Auswertung ergibt sich folgende Tabelle:
| Kaltmiete (pro m) | |
| von …bis unter … | Anzahl |
| 0–6 | 5 |
| 6–8 | 10 |
| 8–10 | 30 |
| 10–13 | 30 |
| 13–16 | 20 |
| 16–20 | 5 |
Bestimmen Sie den Median aus diesen Daten.
Kartoffeln
(Lösung)
An zwei Verladestellen für Kartoffeln der Deutschen Bahn wurden folgende Angaben ermittelt:
| Verlade- | Kosten gesamt | Kosten je | Kosten je verladene Tonne |
| stelle | (EUR) | Stunde (EUR/h) | (EUR/t) |
| 1 | 16 000 | 40 | 1,00 |
| 2 | 27 000 | 45 | 0,75 |
- Berechnen Sie die durchschnittlichen Kosten je verladene Tonne der beiden Verladestellen.
- Wieviel Tonnen wurden durchschnittlich je Stunde bei beiden Verladestellen verladen?
Kaufkurs der Aktien
(Lösung)
Zu Börsenbeginn am gestrigen Tag betrug der Kurs von 4 Aktien, die in Zeile 2 der Tabelle angegebenen Werte. Jemand kaufte zu diesen Kursen die Aktien zu den Kaufbeträgen, die in der Zeile 3 der Tabelle enthalten sind.
| Aktie | A | B | C | D |
|---|---|---|---|---|
| Kurs (in Euro) | 500 | 600 | 400 | 700 |
| Kaufbetrag (in Euro) | 45000 | 84000 | 3600 | 14000 |
Berechnen Sie den mittleren Kaufkurs der Aktien.
Körperschaftssteueraufkommen
(Lösung)
Über das Körperschaftssteueraufkommen einer Stadt, angegeben nach den Rechtsformen der körperschaftssteuerpflichtigen Gesellschaften, sind nachstehende Maßzahlen bekannt:
| Rechtsform | steuer- | mittleres Steuer- | Standard- |
| pflichtige | aufkommen | abweichung | |
| Fälle | (TEUR) | (TEUR) | |
| AG, KGaA | 100 | 9500 | 1000 |
| GmbH | 9500 | 100 | 80 |
| eG | 300 | 200 | 100 |
| sonstige | 100 | 400 | 250 |
Berechnen Sie die Standardabweichung des Körperschaftssteueraufkommens für die gesamte Stadt.
Kontrollzeiten
(Lösung)
An einem Fließband sind sechs Arbeiterinnnen acht Stunden am Tag mit der Kontrolle eines elektronischen Bauteils beschäftigt. Um ein Bauteil zu kontrollieren, benötigen sie folgende Zeiten:
| Arbeiterin | Stückzeit |
|---|---|
| Frau Arbeitsam | 0,2 min |
| Frau Beeilung | 0,4 min |
| Frau Chaos | 0,8 min |
| Frau Durchschnitt | 0,5 min |
| Frau Emsig | 0,5 min |
| Frau Faultier | 0,8 min |
Berechnen Sie die durchschnittliche Kontrollzeit pro Stück an diesem Fließband.
Kurzarbeiter
(Lösung)
Im März wurden in den fünf neuen Bundesländern folgende Anzahlen von Kurzarbeitern nach dem Arbeitsausfall (in %) registriert (fikitve Daten):
| Arbeitsausfall (%) | Anzahl der Kurzarbeiter |
|---|---|
| 10 – 25 | 461 200 |
| 25 – 50 | 687 400 |
| 50 – 75 | 385 200 |
| 75 – 100 | 233 200 |
- Berechnen Sie den durchschnittlichen Arbeitsausfall der Kurzarbeiter im März in den fünf neuen Bundesländern.
- Welcher Arbeitsausfall ergibt sich, wenn 50% der Kurzarbeiter einen geringeren Arbeitsausfall und 50% der Kurzarbeiter einen höheren Arbeitsausfall hatten?
Leichtathletikabteilung
(Lösung)
Die Leichtathletikabteilung des Sportvereins Z ist spezialisiert auf das Training von 100 m – LauferInnen. Nach einem Jahr intensivsten Trainings wurden die Zeiten der 20 LäuferInnen des Vereins gestoppt. Dabei ergab sich folgende Verteilungsfunktion:
- Zeichnen Sie die zur Verteilungsfunktion gehörige Häufigkeitsverteilung.
- Welche Zeit höchstens benötigen die 80% schnellsten Läufer?
- Berechnen Sie die mittlere quadratische Abweichung bezogen auf das arithmetische Mittel und auf den Median.
- Welche Grö“senbeziehung besteht zwischen den beiden Ergebnissen von c)? Gilt diese Grö”senbeziehung stets? Wenn ja, zeigen Sie dies.
Lernzeit
(Lösung)
Ein Universitätspräsident gibt eine statistische Untersuchung in Auftrag, mit der festgestellt werden soll, wie viel Zeit die Studierenden für ihr Studium aufwenden. Die Befragung von 100 Studierenden dieser Universität brachte folgendes Ergebnis:
Keiner der Befragten lernt 12 und mehr Stunden am Tag. Bei 22 Studierenden wurde festgestellt, dass sie sich mindestens 6 Stunden am Tag mit ihrem Studium beschäftigen. Weniger als 3 Stunden am Tag investierten 30% der Befragten in ihr Studium. Die Masse der Studierenden (65%) beschäftigt sich zwischen 3 und 8 Stunden täglich mit Studienangelegenheiten.
- Wie heißt das untersuchte Merkmal und wie ist es skaliert?
- Bestimmen Sie tabellarisch die absoluten und relativen Häufigkeiten und die empirische Verteilungsfunktion. Teilen Sie zu diesem Zweck die Daten in vier Klassen ein.
- Wie viele Stunden höchstens beschäftigt sich genau die Hälfte der Befragten täglich mit dem Studium?
- Wie viele der Befragten arbeiten mindestens 5 Stunden täglich für ihr Studium?
- Wie groß ist der durchschnittliche Zeitaufwand für das Studium bei den 100 befragten Studierenden?
- Welcher Zeitaufwand für das Studium trat bei den befragten Studierenden am häufigsten auf?
Lineares Streuungsmaß
(Lösung)
Von den der Größe nach aufsteigend geordneten fünf Werten eines Merkmals X sind nur die ersten vier lesbar:
| 3 | 7 | 17 | 19 | ?? |
Wie lautet der 5. Wert, wenn bekannt ist, dass die durchschnittliche absolute Abweichung (lineares Streuungsmaß) der fünf Werte – bezogen auf den Median – gleich 8 ist?
Maschinen
(Lösung)
In einer Fabrik stehen zwei Maschinen, die Motorenhauben stanzen: die erste Maschine für den Fiat mit einer durchschnittlichen Länge von 80 cm, die zweite für den Mercedes mit einer durchschnittlichen Länge von 300 cm. Die erste Maschine produziert mit einer Standardabweichung von 4 cm, die zweite mit einer Standardabweichung von 6 cm.
Welche Maschine arbeitet zuverlässiger?
Miete und Wohnfläche
(Lösung)
In einem Wohnviertel mit Häusern verschiedener Wohnungseigentümer wird die Quadratmetermiete in Abhängigkeit von der Wohnfläche analysiert. Es ergibt sich aus der Auswertung von 10 Mietwohnungen folgendes Bild:
| Wohnfläche (m) | ||||
| 40 | 12 | 12 | 15 | |
| 60 | 12 | |||
| 80 | 10 | 10 | ||
| 90 | 9 | 10 | 10 | 10 |
Der Makler möchte wissen, wie die Abhängigkeit von Miete und Wohnfläche ist. Bestimmen Sie für ihn die Kovarianz der Merkmale.
Minimale Summe
(Lösung)
Für ein metrisches Merkmal hat man folgende Urliste
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| 5 | 7 | 9 | 10 | 10 | 12 | 13 | 14 |
Für welche reelle Zahl ist minimal? (ohne Beweis!)
Nelkenstrauß
(Lösung)
Ein Kunde kauft an einem Tag einen Strau“s Nelken für 12 EUR, das Stück zu 0,80 EUR, und am nächsten Tag einen Strau”s Nelken für 26 EUR, das Stück zu 1,04 EUR. Welcher durchschnittliche Preis ist für eine Nelke an diesen beiden Tagen bezahlt worden?
Neubauwohnungen
(Lösung)
Über die Bauzeiten der im Jahre in der Stadt C errichteten Neubauwohnungen liegen folgende Angaben vor:
| Bauzeit | Anteil der neugebauten |
| (in Monaten) | Wohnungseinheiten (in Prozent) |
| 2–4 | 3,7 |
| 4–6 | 13,1 |
| 6–8 | 27,5 |
| 8–10 | 21,1 |
| 10–12 | 16,0 |
| 12–14 | 6,4 |
| 14–16 | 5,3 |
| 16–18 | 6,9 |
Berechnen Sie drei aussagekräftige Mittelwerte zur Beantwortung der Frage:
Wie viele Monate Bauzeit wurden im Mittel für die im Jahre in der Stadt C errichteten Wohnungseinheiten benötigt?
Perlenkette
(Lösung)
Agathe hat von ihrem Freund eine Perlenkette geschenkt bekommen. Um sich einen Überblick über den Wert der Kette zu verschaffen, misst sie die Durchmesser (in mm) der Perlen:
| 3,1 | 4,2 | 3,7 | 6,8 | 7,3 | 5,2 | 5,4 | 4,5 | 3,9 | 3,3 |
| 5,0 | 3,7 | 6,9 | 6,1 | 4,0 | 4,1 | 6,1 | 6,0 | 5,7 | 5,2 |
| 5,6 | 4,4 | 4,2 | 3,7 | 5,3 | 3,4 | 6,8 | 6,3 | 4,1 | 3,3 |
| 4,2 | 5,8 | 5,6 | 3,2 | 5,5 | 4,5 | 5,1 | 4,6 | 5,3 | 3,4 |
| 6,5 | 6,2 | 4,0 | 3,6 | 4,9 | 4,8 | 4,9 | 4,6 | 4,7 | 4,8 |
| 4,5 | 5,4 | 3,5 | 5,8 | 4,9 | 5,0 | 3,6 | 7,5 | 3,2 | 3,2 |
| 3,4 | 3,5 | 3,2 | 5,1 | 5,5 | 4,3 | 4,5 | 3,8 | 5,1 | 3,8 |
| 7,2 | 5,9 |
- Erstellen Sie eine Häufigkeitstabelle bei Zugrundelegung von Klassen mit 1 mm Klassenbreite.
- Berechnen Sie basierend auf den klassierten Daten den durchschnittlichen Durchmesser der Perlen.
- Welcher Durchmesser trat bei dieser Perlenkette am häufigsten auf?
- Welchen Durchmesser höchstens haben 50% der kleinsten Perlen?
Produktionsleistung einer Maschine
(Lösung)
An einer neu angeschafften Maschine, die pro Tag maximal 300 Produkteinheiten herstellen kann, werden an insgesamt 20 Tagen folgende Stückzahlen produziert:
| Anzahl der Tage | 6 | 3 | 5 | 4 | 2 |
|---|---|---|---|---|---|
| produzierte Stück/Tag | 296 | 297 | 298 | 295 | 299 |
- Der Abteilungsleiter behauptet gegenüber dem Firmenchef, dass die Maschine im Durchschnitt pro Tag über 98% ihrer Produktionsleistung erbringt. Überprüfen Sie diese Aussage!
- Berechnen Sie den Median und die mittlere absolute Abweichung vom Median der produzierten Stückzahlen/Tag.
Reinigungsunternehmen - Teil I
(Lösung)
Für die Angestellten der drei Putzkolonnen eines Reinigungsunternehmens ergeben sich aufgrund von Alter, Betriebszugehörigkeit und Einsatzgebiet folgende Einkommen (in EUR) pro Monat:
- 2 624, 2 830, 2 386, 2 395, 2 147, 2 546
- 2 936, 2 758, 2 774, 2 822
- 2 325, 2 536, 2 395, 2 454, 2 640.
Berechnen Sie für jede Putzkolonne und für das gesamte Reinigungsunternehmen das durchschnittliche Einkommen und den Median des Einkommens.
Reinigungsunternehmen - Teil II
(Lösung)
Berechnen Sie für jede Putzkolonne aus der Aufgabe davor die Standardabweichung und den Variationskoeffizienten.
Ermitteln Sie anschließend unter Verwendung dieser Varianzen die Varianz des zusammengesetzten Datensatzes, d.h. die Varianz für das gesamte Reinigungsunternehmen.
Sanatorium
(Lösung)
In einem Sanatorium wird ein kleiner Wettlauf der Patienten über 50m durchgeführt. Die folgende Tabelle gibt in der Reihenfolge ihres Eintreffens am Ziel das Gewicht (in kg) der Patienten an:
| Patient | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Gewicht | 70 | 60 | 80 | 77 | 82 | 81 | 78 | 100 | 83 | 110 | 79 |
- Wie stark ist der Zusammenhang zwischen Körpergewicht und Laufleistung?
- Bestimmen Sie den Median des Körpergewichts.
- Bestimmen Sie das quadratische Streuungsmaß in Bezug auf den Median.
- Ist die Varianz des Gewichts grö“ser oder kleiner als die unter c) bestimmte Grö”se? Warum?
- Die zwei Frauen unter den Patienten liefen die Strecke mit Geschwindigkeiten von 2 bzw. 4 Meter pro Sekunde. Wie groß war die Durchschnittsgeschwindigkeit der Frauen?
Schafzucht - Teil I
(Lösung)
Der schottische Großgrundbesitzer McDuff verdient sein Geld mit der Zucht von Schafen. Er nimmt sich für die nächste Schafsschur vor, sowohl billige irische Wanderarbeiter mit einem Leistungslohn von 15 Pfund pro kg Wolle, als auch einheimische Arbeiter für 20 Pfund pro kg Wolle einzusetzen. Für die Iren will er insgesamt 285 Pfund, für die Schotten insgesamt 260 Pfund an Lohnsumme aufbringen.
Wie hoch sind seine durchschnittlichen Lohnkosten pro kg Wolle?
Schafzucht Teil - II
(Lösung)
Fortsetzung der Aufgabe davor. Unser schottischer Großgrundbesitzer McDuff (aus Aufgabe 33) verkauft die Wolle an einen Freund auf den Niederländischen Antillen. Im Laufe der letzten fünf Monate erwirtschaftete er folgende Gewinne (in Tsd. Gulden): 5 ; 4 ; 20 ; 6 ; 4.
McDuff tauscht sein Geld stets bei einem Bankier in Edinburgh in Pfund ein. Er weiß, dass der Wechselkurs stabil ist und er jeden Monat eine feste, vom Umtauschbetrag unabhängige Gebühr zu entrichten hat. In den letzten fünf Monaten hat er insgesamt 15,5 (Tsd.) Pfund ausgezahlt bekommen. Die Varianz betrug 9,44 (Tsd. Pfund).
Wie hoch sind Gebühr und Wechselkurs?
Schulbezirke
(Lösung)
Aus einem Datensatz mit nicht klassierten Daten über 506 Schulbezirke in einer Großstadt wurden folgende Variablen zur Analyse ausgewählt:
- : der Schulbezirk liegt verkehrsgünstig (1) oder nicht (0)
- : durchschnittliche Anzahl von Räumen pro Haus im Schulbezirk
Für diese Variablen wurden folgende Maßzahlen berechnet:
| Maßzahl | ||
|---|---|---|
| arithmetischer Mittelwert | 0,07 | 6,28 |
| Maximum | 1,00 | 8,78 |
| Median | 0,00 | 6,21 |
| Minimum | 0,00 | 3,56 |
| Modus | 0,00 | 5,71 |
| Spannweite | 1,00 | 5,22 |
| Standardabweichung | 0,00 | 0,70 |
| Varianz | 0,07 | 0,49 |
| 25%-Quartil | 0,00 | 5,88 |
| 75%-Quartil | 0,00 | 6,63 |
Begründen Sie kurz, welche Maßzahlen für welche Variable sinnvoll sind.
Streuungsmaß
(Lösung)
Gegeben sind Beobachtungswerte eines Merkmals X. Zur Konstruktion eines Streuungsmaßes sollen die absoluten (d.h. ohne Berücksichtigung des Vorzeichens) Abweichungen eines jeden Beobachtungswertes von jedem anderen Beobachtungswert ermittelt werden.
- Wie groß ist die Anzahl der zu ermittelnden absoluten Abweichungen? Begründen Sie diese Anzahl mittels der Kombinatorik.
- Welche Skalierung ist für das Merkmal X erforderlich, um ein solches Streuungsmaß zu konstruieren?
Tägliche Arbeitswege - Teil I
(Lösung)
Der Direktor einer Bank möchte sich über die täglich anfallenden Anfahrtswege seiner Mitarbeiter zum Arbeitsplatz informieren. Von der Personalabteilung wird ihm auf seine Anfrage folgende Tabelle übersandt.
| Anfahrtsweg (km) | Anzahl der |
| Beschäftigten | |
| 0 – 1 | 7 |
| 1 – 5 | 24 |
| 5 – 15 | 35 |
| 15 – 30 | 18 |
| 30 – 50 | 16 |
- Nennen Sie die statistischen Einheiten und das untersuchte statistische Merkmal. Wie ist das Merkmal skaliert?
- Ermitteln Sie die absoluten und relativen Häufigkeiten, die Häufigkeitsdichten und die empirische Verteilungsfunktion. Stellen Sie die Häufigkeitsverteilung und die empirische Verteilungsfunktion graphisch dar.
- Berechnen Sie den durchschnittlichen Anfahrtsweg.
- Welcher Anfahrtsweg tritt bei den Beschäftigten dieser Bank am häufigsten auf? Wie wird dieser Parameter genannt?
- Welcher Anfahrtsweg ergibt sich, wenn 50% der Beschäftigten einen kürzeren bzw. 50% einen weiteren Anfahrtsweg haben?
- Berechnen Sie die p–Quantile für .
Tägliche Arbeitswege - Teil II
(Lösung)
Berechnen Sie, ausgehend von der Aufgabe davor
- den Quartilsabstand
- die mittlere absolute Abweichung vom Median
des Anfahrtsweges/Beschäftigter der betrachteten Bank.
Tarifverhandlungen
(Lösung)
Ein Großunternehmen veröffentlicht folgende Angaben über die Verteilung der Jahresbruttolöhne seiner Lohnempfänger im Jahre 2011: Von den insgesamt 20000 Lohnempfängern bezogen 16000 einen Jahresbruttolohn von mindestens 9600 EUR. Der durchschnittliche Jahresbruttolohn betrug 21200 EUR.
Bei den nächsten Tarifverhandlungen wird folgendes vereinbart: Alle Lohnempfänger erhalten 5% mehr Bruttolohn. Weiter erhalten alle Lohnempfänger mit einem bisherigen Bruttolohn unter 9600 EUR zusätzlich einen Festbetrag von jährlich 200 EUR mehr.
Unterstellen Sie, dass außer den vereinbarten Tarifänderungen keine weiteren Anderungen (Zahl und Struktur der Lohnempfänger, Klasseneinteilung) eintreten.
Wie groß ist dann der durchschnittliche Jahresbruttolohn nach dem Tarifabschluß?
Tekolom und IBBM - Teil I
(Lösung)
Herr Sparsam besaß im letzten Jahr Aktien der Firma Tekolom und IBBM. Für die beiden Aktien ist die folgende gemeinsame Häufigkeitsverteilung beobachtet worden:
| Anzahl | Kurs der | Kurs der |
| der Tage | Tekolom-Aktie | IBBM-Aktie |
| 73 | 35 EUR | 120 EUR |
| 146 | 40 EUR | 130 EUR |
| 146 | 45 EUR | 125 EUR |
Stellen Sie fest, ob die Kurse der beiden Aktien korreliert sind. Berechnen Sie den Korrelationskoeffizienten nach Bravais–Pearson.
Telefonanbieter
(Lösung)
Familie Sparsam nutzt fleißig die Niedrigpreise verschiedener Telefonanbieter. Im Monat Februar 2015 ergibt ihre Telefonrechnung folgende Daten für Ferngespräche:
| Anbieter | Minutenpreis | Rechnungsbetrag |
| (in EUR) | (in EUR) | |
| 0,10 | 20,00 | |
| 0,15 | 11,25 | |
| 0,19 | 47,50 |
Berechnen Sie den von Familie Sparsam im Februar bezahlten Durchschnittspreis für eine Minute Ferngespräch.
Telefon–Interviews
(Lösung)
Eine Marketing-Firma führt häufig Telefon-Interviews in Berlin durch. Hierbei werden folgende Entgelte an die Telekom bezahlt: im Tagestarif (9-18 Uhr) 12 Cent/90 Sekunden und im Freizeittarif (5-9 Uhr und 18-21 Uhr) 12 Cent/150 Sekunden.
Es soll ausdrücklich darauf hingewiesen werden, dass bei der Telekom jede angefangene 90– bzw. 150–Sekundeneinheit voll bezahlt werden muss.
Die Interviews dauern entweder genau 10 oder genau 20 Minuten. An einem zufällig ausgewählten Tag werden die Telefongespräche wie folgt geführt:
| Zeitbereich | 10-Min.-Interviews | 20-Min.-Interviews |
|---|---|---|
| 7-8 Uhr | 3 | 1 |
| 11-14 Uhr | 10 | 20 |
| 19-20 Uhr | 15 | 10 |
Wie hoch sind die mittleren Telefonkosten für ein Interview an diesem Tag?
Tennis Turniere
(Lösung)
Tennis–As B.B. blickt auf eine völlig missglückte Saison zurück. Insgesamt nahm er an 40 Turnieren in aller Welt teil. Jedes Turnier ging über 6 Runden:
1. Runde
2. Runde
3. Runde = Achtelfinale
4. Runde = Viertelfinale
5. Runde = Halbfinale
6. Runde = Finale
Gespielt wurde in jeder Runde im k.o.–Verfahren, d.h. der Spieler, der seine Partie verlor, schied aus.
Die Bilanz seiner Turnierergebnisse lässt keine Freude bei B.B. aufkommen: Er stand zweimal im Finale und wurde sechsmal erst im Halbfinale von seinem Gegner geschlagen. Zehnmal verlor er jedoch schon in der ersten Runde und sechzehnmal kam für ihn in der 2. Runde das Aus. In der dritten Runde schied er allerdings bei keinem Turnier aus.
- Wie heißt das untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret?
- Bestimmen Sie tabellarisch die absoluten und relativen Häufigkeiten und die empirische Verteilungsfunktion.
- Zeichnen Sie die empirische Verteilungsfunktion.
- Bei wieviel Prozent der Turniere schied B.B. vor dem Achtelfinale aus?
- Bei wieviel Prozent der Turniere erreichte B.B. mindestens das Halbfinale?
- Bei wie vielen Turnieren spielte B.B. noch in der 2. Runde mit?
- In welcher Runde spätestens schied B.B. bei 80% der Turniere aus?
- In welcher Runde schied B.B. bei genau 40% der Turniere aus?
- Interpretieren Sie – bezogen auf den Aufgabentext – kurz den Funktionswert an der Stelle .
Walzabteilung
(Lösung)
In einer Walzabteilung bedienen 4 Arbeiter (A, B, C und D) unterschiedlich moderne Maschinen. Sie benötigen jeweils folgende Durchschnittszeiten zum Walzen eines Stückes Blech:
| A: 20 Sek/Stück | B: 30 Sek/Stück |
| C: 60 Sek/Stück | D: 60 Sek/Stück |
I. Betrachten Sie die Variable X: “Bearbeitungszeit in sec/Stück”.
Angenommen die Arbeiter arbeiten gleichlange, welche Durchschnittszeit pro Stück wird in der Abteilung benötigt?
Angenommen den Arbeitern sind folgende Stückkontingente vorgegeben:
A: 1000 Stück B: 500 Stück C: 300 Stück D: 200 Stück welche Durchschnittszeit pro Stück wird in der Abteilung jetzt benötigt?
II. Betrachten Sie die Variable Y: “hergestellte Stück pro Stunde”.
- Angenommen die Arbeiter arbeiten gleichlange, wie viel Stück werden im Durchschnitt pro Stunde gewalzt?
- Angenommen den Arbeitern sind die Stückkontingente von I b) vorgegeben, wie viel Stück pro Stunde werden jetzt im Durchschnitt gewalzt?
Wanderer
(Lösung)
Ein Wanderer legte 2 Kilometer zurück. Den ersten Kilometer ging er mit einer Geschwindigkeit von 6 km je Stunde, den zweiten mit einer Geschwindigkeit von 4 km je Stunde.
Wie groß war seine Durchschnittsgeschwindigkeit?
WM–Berichterstattung
(Lösung)
Um festzustellen, wie viele Stunden pro Spieltag ein Fu“sball–Fan die WM–Berichterstattung im Fernsehen während der letzten Fu”sball–WM verfolgte, wurden 20 Fußball–Fans in A–Dorf nach ihrem Fernsehkonsum während der WM befragt. Die Befragung brachte folgendes Ergebnis:
| Stunden | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| relative Häufigkeit | 0.05 | 0.1 | 0.4 | 0.2 | 0.25 |
- Wie lautet das hier untersuchte statistische Merkmal und wie ist es skaliert? Ist es häufbar, nicht häufbar, stetig oder diskret?
- Bestimmen Sie tabellarisch die absoluten und relativen Häufigkeiten und die empirische Verteilungsfunktion.
- Wieviele Stunden sehen 10% der Befragten höchstens fern?
- Geben sie an, wieviele Stunden 85% der Befragten mindestens fernsehen.
- Geben Sie die Stundenzahl an, die genau 20% der Befragten fernsehen.
Zigaretten
(Lösung)
Im Rahmen einer medizinischen Untersuchung in S–Stadt im Januar wurden 200 Personen zufällig befragt, wieviele Zigaretten sie pro Tag rauchen. Das Ergebnis dieser Untersuchung sei in folgender Graphik beschrieben:
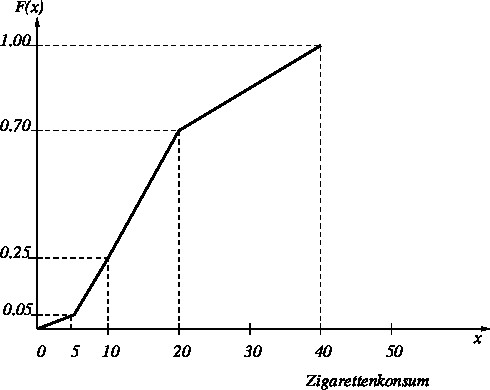
- Wie heißt die obige Darstellungsform? Welche Annahmen wurden hinsichtlich der Verteilung innerhalb jeder Klasse getroffen?
- Geben Sie die absoluten und relativen Klassenhäufigkeiten, die Häufigkeitsdichten und die empirische Verteilungsfunktion an.
- Geben Sie an, wie hoch der Anteil der Befragten ist, die mindestens 20 Zigaretten pro Tag rauchen.
Zuckergewicht
(Lösung)
Das Füllgewicht von 75 maschinell abgepackten Paketen Zucker wurde kontrolliert. Die Messwerte ergeben folgende Häufigkeitsverteilung:
| Füllgewicht (in g) | Anzahl der Pakete |
|---|---|
| 980 – 990 | 5 |
| 990 – 995 | 12 |
| 995 – 1000 | 23 |
| 1000 – 1005 | 22 |
| 1005 – 1010 | 11 |
| 1010 – 1020 | 2 |
Berechnen Sie den Modus, den Median und das arithmetische Mittel des Füllgewichts.
Zugfolge - Teil I
(Lösung)
An einer Schranke der Bahnstrecke von A nach B wurden am 20.1.folgende Abstände der Zugfolge in Minuten gemessen:
59; 43; 36; 63; 23; 4; 29; 41; 43; 31; 29; 69; 57; 36; 112; 43; 14; 11; 18; 77; 81; 47; 12; 43; 44; 16; 80; 6; 52; 5; 5; 6; 21; 43; 44; 46; 51
- Wie ist das Erhebungsmerkmal skaliert? Ist es häufbar, nicht häufbar, stetig, diskret?
- Ermitteln Sie die absolute und relative Klassenhäufigkeiten unter Verwendung von Klassen der Breite 30 Minuten. Stellen Sie die Häufigkeitsverteilung graphisch dar.
- Geben Sie die empirische Verteilungsfunktion an und stellen Sie diese graphisch dar.
Zugfolge - Teil II
(Lösung)
- Berechnen Sie aufgrund der Häufigkeitsverteilung der klassierten Daten für das Erhebungsmerkmal : “Zugfolgeabstand” der Aufgabe davor drei aussagekräftige Lageparameter.
- Welcher durchschnittlicher Zugfolgeabstand ergibt sich auf der Basis der Urliste? Wie erklären Sie sich den Unterschied zum zahlenmäßigen Ergebnis des gleichen Mittelwertes aus Frage a)?