Zeitreihenanalyse: Unterschied zwischen den Versionen
Aus MM*Stat
(→PKW) |
|||
| Zeile 65: | Zeile 65: | ||
Tägliche Temperaturen in New York, Mai bis September 1973 | Tägliche Temperaturen in New York, Mai bis September 1973 | ||
<iframe k="wiwi" p="examples/stat_Zeitreihenanalyse_temperaturNY_R00480004800000000000000_plot.html" /> | |||
===Passagiere=== | ===Passagiere=== | ||
Version vom 7. April 2019, 14:07 Uhr
Grundbegriffe
Zeitreihenanalyse und Zeitreihen
Eine Zeitreihe zeichnet die Ausprägungen eines Merkmals (einer Variablen) im Zeitverlauf auf.
Die Betrachtung der Zeitreihen in den unten stehenden Beispielen lässt erkennen, wie unterschiedlich die zeitliche Entwicklung der Merkmalsausprägungen sein kann.
Diese verschiedenen Eigenschaften im jeweiligen Anwendungsfall zu erfassen, ist das Ziel der deskriptiven Analyse. Deskriptive Zeitreihenmodelle werden so gewählt, dass sie die Charakteristika der Reihe verdeutlichen.
Zeitreihen können auch als Ergebnis eines stochastischen Prozesses interpretiert werden. Vor diesem Hintergrund versucht man stochastische Modelle zu finden, die zu den Beobachtungen geführt haben könnten.
Besonderes Gewicht kommt hierbei der Identifikation von Einflussfaktoren, die häufig ebenfalls Zeitreihen sind, zu.
Ein stochastisches Zeitreihenmodell kann helfen, den Prozess, der zu den Beobachtungen geführt hat, zu verstehen.
Wenn man ferner annimmt, dass das Modell auch in der Zukunft noch gelten wird, ermöglicht es Voraussagen zukünftiger Merkmalsausprägungen.
Im folgenden werden nur deskriptive Zeitreihenmodelle betrachtet.
Komponenten einer Zeitreihe
Um ihre charakteristischen Eigenschaften offenzulegen, zerlegt man Zeitreihen häufig in Bewegungskomponenten:
- Allgemeine Tendenz der Zeitreihe.
- Kurzfristige Einflüsse, die nach einem starren Muster die langfristige Entwicklung überlagern. Die Periodenlänge beträgt häufig ein Jahr, in diesem Fall spricht man von Saisonschwankungen.
- Unregelmäßige Restschwankungen
Der Trend und Saisonschwankung gelten als systematische Komponenten und werden in den folgenden Unterkapiteln weiter diskutiert.
Beispiele
Scatterplots geben einen Eindruck von der Entwicklung der Merkmalsausprägungen im Zeitverlauf.
Auf der Abzisse werden Indikatoren für den jeweiligen Beobachtungszeitpunkt (z.B. Jahreszahlen) abgetragen, die Ordinate gibt die zugehörige Merkmalswerte an.
Wie die folgenden Beispiele illustrieren, finden sich Zeitreihen in den verschiedensten Wissensgebieten:
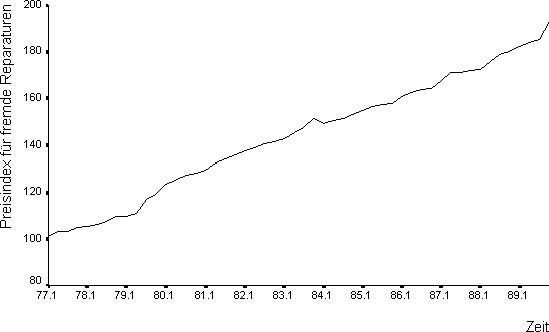
Reparaturen
Preisindex für fremde Reparaturen und sonstige Dienstleistungen Berlin, 1. Quartal 1977 - 4. Quartal 1989
Telefone
Anzahl der Telefone in den USA (in 1000) 1900 - 1970
PKW
Zulassungszahl neuer PKW in Berlin 1. Quartal 1977 - 4. Quartal 1989
Temperaturen
Tägliche Temperaturen in New York, Mai bis September 1973
Passagiere
Anzahl der Passagiere der amerikanischen Flug-Gesellschaft Pan Am Januar 1949 - Dezember 1960
| <R output="display">
pdf(rpdf, width=10, height=7) data(AirPassengers) AP = AirPassengers par(mar=c(5, 7, 1, 2) + 0.1) par(mgp = c(3, 1, 0)) plot(AP, xlab="Zeit", ylab="Anzahl der Passagiere einer Flug-Gesellschaft (Tsd.)", axes=F, col="brown", lwd=3) axis(1, tck=-0.02, at=seq(1949.083, 1961.083, by=1), label=seq(49.1, 61.1, by=1), cex.axis=0.85) axis(2, tck=-0.02, las=2) </R> |