|
|
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| | {{Zeitreihen}} |
| | |
| =={{Vorlage:Überschrift}}== | | =={{Vorlage:Überschrift}}== |
|
| |
|
| Zeile 231: |
Zeile 233: |
| <math>\widehat{x}_{t}=3578,04\cdot (1,051)^{t}</math> | | <math>\widehat{x}_{t}=3578,04\cdot (1,051)^{t}</math> |
|
| |
|
| {|
| | <iframe k="wiwi" p="examples/stat_Trend_Anzahl_Telefone_R00480004800000000000000_plot.html" /> |
| |<R output="display">
| |
| | |
| pdf(rpdf, width=10, height=7)
| |
| | |
| S = c(1355900, 1801100, 2371044, 2808900, 3353200, 4126900, 4932800, 6118578, 6483600, 6995700, 7635400, 8348700, 8729592, 9542500, 10046400, 10523500, 11241400, 11716520, 12077600, 12668500, 13411400, 13875200, 14347395, 15369500, 16208900, 16935900, 17746200, 18522767, 19341300, 20233000, 20201600, 19707600, 17424406, 16710900, 16968800, 17424000, 18433000, 19453401, 19953000, 20831000, 21928000, 23521000, 24919000, 26381000, 26859000, 27867000, 31611000, 34867000, 38205000, 40708000, 43003800, 45636400, 48056300, 50373000, 52813000, 56243200, 60190400, 63620900, 66629600, 70819000, 74341100, 77425400, 80971700, 84450300, 88787400, 93658800, 98785600, 103751900, 109255600, 115200700, 120221000);
| |
| tel = ts(S, start=1900, end=1970, fr=1)
| |
| par(mar=c(5, 7, 1, 2) + 0.1)
| |
| par(mgp = c(3, 1, 0))
| |
| plot(tel, lwd=3, col="blue", axes=F, xlab="Jahr", ylab="", ylim=c(0, 140000000))
| |
| axis(1, tck=-0.02)
| |
| options(scipen=5)
| |
| axis(2, at=seq(0, 140000000, by=20000000), label=seq(0, 140000, by=20000), las=2, tck=-0.02)
| |
| par(mgp = c(5, 1, 0))
| |
| title(ylab="Anzahl der Telefone in USA (1000)")
| |
| t = as.numeric(time(tel)-1900)
| |
| tel.lm = lm(log(tel)~t)
| |
| lines(exp(tel.lm$coef[1]+tel.lm$coef[2]*(time(tel)-1900)), col="red", lwd=3)
| |
| | |
| </R>
| |
| | |
| |}
| |
|
| |
|
| ===PKW (Symmetrischer Filter)=== | | ===PKW (Symmetrischer Filter)=== |
| Zeile 264: |
Zeile 245: |
| schwarz: geglättete Reihe (Trend) | | schwarz: geglättete Reihe (Trend) |
|
| |
|
| {|
| | <iframe k="wiwi" p="examples/stat_Trend_Zulassung_PKW_R00480004800000000000000_plot.html" /> |
| |<R output="display">
| |
| | |
| pdf(rpdf, width=10, height=7)
| |
| | |
| a = c(15222, 17456, 12988, 13833, 15407, 19110, 13479, 13139, 16407, 18738, 11923, 11853, 15869, 16109, 12883, 11712, 14495, 15373, 10341, 11111, 12985, 13397, 9474, 10043, 13431, 15968, 11246, 11261, 14908, 14581, 10498, 10657, 11078, 14858, 11473, 12384, 13801, 17143, 14249, 14712, 12603, 16799, 15611, 15568, 13077, 17098, 14159, 13085, 14093, 16344, 12044, 13762)
| |
| t = ts(a, start=c(1977,1), end=c(1989,4), fr=4)
| |
| plot(t, ylim=c(8000,20000), xlab="Zeit", ylab="Zulassungszahl neuer Pkw (Tsd.)", col="red", lwd=3, axes=F)
| |
| axis(1, at=seq(1977.1, 1989.4, by=1.0), label=seq(77.1, 89.4, by=1.0), tck=-0.02)
| |
| axis(2, at=seq(8000, 20000, by=2000), label=seq(8, 20, by=2), las=2, tck=-0.02)
| |
| lines(decompose(t)$trend, lwd=3)
| |
| | |
| </R>
| |
| |}
| |
|
| |
|
| ===Leistungsbilanzsalden=== | | ===Leistungsbilanzsalden=== |
| Zeile 297: |
Zeile 265: |
| In der folgenden Tabelle wurde der gleitende Durchschnitt <math>T(t)</math> jeweils für <math>a=1,\; a=2</math> und <math>a=3\;</math> berechnet. | | In der folgenden Tabelle wurde der gleitende Durchschnitt <math>T(t)</math> jeweils für <math>a=1,\; a=2</math> und <math>a=3\;</math> berechnet. |
|
| |
|
| {| border="1" cellpadding="3" style="text-align:center;margin:1em 1em 1em 0; background:#f9f9f9; border:1px #AAA solid; border-collapse:collapse; empty-cells:show;" | | |
| |align="center" rowspan="2"|Jahr | | {| class="wikitable" |
| |align="center" rowspan="2"|<math>t</math> | | |-align="center" |
| |align="center" rowspan="2"|Leistungsbilanz | | | rowspan="2"|Jahr |
| |align="center"|<math>T(t)</math>
| | | rowspan="2"|<math>t</math> |
| |align="center"|<math>T(t)</math>
| | | rowspan="2"|Leistungsbilanz |
| |align="center"|<math>T(t)</math>
| | |<math>T(t)</math> |
| |- | | |<math>T(t)</math> |
| |align="center"|<math>a=1</math>
| | |<math>T(t)</math> |
| |align="center"|<math>a=2</math>
| | |- align="center" |
| |align="center"|<math>a=3</math>
| | |<math>a=1</math> |
| |- | | |<math>a=2</math> |
| |align="center"|1977
| | |<math>a=3</math> |
| |align="center"|1 | | |- align="right" |
| |align="center"|9478 | | |1977 |
| |align="center"| | | |1 |
| |align="center"| | | |9478 |
| |align="center"| | | | |
| |- | | | |
| |align="center"|1978 | | | |
| |align="center"|2 | | |- align="right" |
| |align="center"|18003 | | |1978 |
| |align="center"|5483,3 | | |2 |
| |align="center"| | | |18003 |
| |align="center"| | | |5483,3 |
| |- | | | |
| |align="center"|1979 | | | |
| |align="center"|3 | | |- align="right" |
| |align="center"|-11031 | | |1979 |
| |align="center"|-7169,3 | | |3 |
| |align="center"|-4754,2 | | | -11031 |
| | | -7169,3 |
| | | -4754,2 |
| | | |
| | |- align="right" |
| | |1980 |
| | |4 |
| | | -28480 |
| | | -17084,0 |
| | | -4676,6 |
| | | -476,0 |
| | |- align="right" |
| | |1981 |
| | |5 |
| | | -11741 |
| | | -10118,3 |
| | | -6162,6 |
| | |2161,4 |
| | |- align="right" |
| | |1982 |
| | |6 |
| | |9866 |
| | |2899,3 |
| | |1631,6 |
| | |6493,4 |
| | |- align="right" |
| | |1983 |
| | |7 |
| | |10573 |
| | |16126,3 |
| | |16993,0 |
| | |20325,4 |
| | |- align="right" |
| | |1984 |
| | |8 |
| | |27940 |
| | |28946,7 |
| | |36499,8 |
| | |36122,1 |
| | |- align="right" |
| | |1985 |
| | |9 |
| | |48327 |
| | |54020,0 |
| | |50946,0 |
| | |50418,9 |
| | |- align="right" |
| | |1986 |
| | |10 |
| | |85793 |
| | |72072,3 |
| | |66498,6 |
| | |63874,7 |
| | |- align="right" |
| | |1987 |
| | |11 |
| | |82097 |
| | |85408,7 |
| | |81722,0 |
| | |64551,3 |
| | |- align="right" |
| | |1988 |
| | |12 |
| | |88336 |
| | |91496,7 |
| | |75118,4 |
| | |56000,4 |
| | |- align="right" |
| | |1989 |
| | |13 |
| | |104057 |
| | |69234,0 |
| | |51576,6 |
| | |44779,3 |
| | |- align="right" |
| | |1990 |
| | |14 |
| | |15309 |
| | |29150,0 |
| | |29113,0 |
| | |29186,0 |
| | |- align="right" |
| | |1991 |
| | |15 |
| | | -31916 |
| | | -15609,3 |
| | |6774,4 |
| | |12573,9 |
| | |- align="right" |
| | |1992 |
| | |16 |
| | | -30221 |
| | | -28498,0 |
| | | -20875,2 |
| | | -4876,7 |
| | |- align="right" |
| | |1993 |
| | |17 |
| | | -23357 |
| | | -29256,3 |
| | | -30700,6 |
| | | | | |
| |- | | |- align="right" |
| |align="center"|1980
| | |1994 |
| |align="center"|4
| | |18 |
| |align="center"|-28480
| | | -34191 |
| |align="center"|-17084
| | | -30455,3 |
| |align="center"|-4676,6
| |
| |align="center"|-476
| |
| |-
| |
| |align="center"|1981
| |
| |align="center"|5
| |
| |align="center"|-11741
| |
| |align="center"|-10118,3
| |
| |align="center"|-6162,6
| |
| |align="center"|2161,4
| |
| |-
| |
| |align="center"|1982
| |
| |align="center"|6
| |
| |align="center"|9866
| |
| |align="center"|2899,3
| |
| |align="center"|1631,6
| |
| |align="center"|6493,4
| |
| |-
| |
| |align="center"|1983
| |
| |align="center"|7
| |
| |align="center"|10573
| |
| |align="center"|16126,3
| |
| |align="center"|16993
| |
| |align="center"|20325,4
| |
| |-
| |
| |align="center"|1984
| |
| |align="center"|8
| |
| |align="center"|27940
| |
| |align="center"|28946,7
| |
| |align="center"|36499,8
| |
| |align="center"|36122,1
| |
| |-
| |
| |align="center"|1985
| |
| |align="center"|9
| |
| |align="center"|48327
| |
| |align="center"|54020
| |
| |align="center"|50946
| |
| |align="center"|50418,9
| |
| |-
| |
| |align="center"|1986
| |
| |align="center"|10
| |
| |align="center"|85793
| |
| |align="center"|72072,3
| |
| |align="center"|66498,6
| |
| |align="center"|63874,7
| |
| |-
| |
| |align="center"|1987
| |
| |align="center"|11
| |
| |align="center"|82097
| |
| |align="center"|85408,7
| |
| |align="center"|81722
| |
| |align="center"|64551,3
| |
| |-
| |
| |align="center"|1988
| |
| |align="center"|12
| |
| |align="center"|88336
| |
| |align="center"|91496,7
| |
| |align="center"|75118,4
| |
| |align="center"|56000,4
| |
| |-
| |
| |align="center"|1989
| |
| |align="center"|13
| |
| |align="center"|104057
| |
| |align="center"|69234
| |
| |align="center"|51576,6
| |
| |align="center"|44779,3
| |
| |-
| |
| |align="center"|1990
| |
| |align="center"|14
| |
| |align="center"|15309
| |
| |align="center"|29150
| |
| |align="center"|29113
| |
| |align="center"|29186
| |
| |-
| |
| |align="center"|1991
| |
| |align="center"|15
| |
| |align="center"|-31916
| |
| |align="center"|-15609,3
| |
| |align="center"|6774,4
| |
| |align="center"|12573,9
| |
| |-
| |
| |align="center"|1992
| |
| |align="center"|16
| |
| |align="center"|-30221
| |
| |align="center"|-28498
| |
| |align="center"|-20875,2
| |
| |align="center"|-4876,7
| |
| |-
| |
| |align="center"|1993
| |
| |align="center"|17
| |
| |align="center"|-23357
| |
| |align="center"|-29256,3
| |
| |align="center"|-30700,6
| |
| |align="center"|
| |
| |-
| |
| |align="center"|1994
| |
| |align="center"|18
| |
| |align="center"|-34191
| |
| |align="center"|-30455,3
| |
| | | | | |
| | | | | |
| |- | | |- align="right" |
| |align="center"|1995
| | |1995 |
| |align="center"|19
| | |19 |
| |align="center"|-33818
| | | -33818 |
| | | | | |
| | | | | |
| | | | | |
| |} | | |} |
| | |
|
| |
|
| Wenn <math>a = 1</math> ist, kann man für die Periode <math>t = 1</math> keinen Trend [[Schätzung|schätzen]], weil der Wert der [[Zeitreihe]] in <math>t = 0</math> unbekannt ist. | | Wenn <math>a = 1</math> ist, kann man für die Periode <math>t = 1</math> keinen Trend [[Schätzung|schätzen]], weil der Wert der [[Zeitreihe]] in <math>t = 0</math> unbekannt ist. |
| Zeile 449: |
Zeile 420: |
| In der folgenden Grafik werden die drei [[Schätzung]]en und die Originalreihe miteinander verglichen: | | In der folgenden Grafik werden die drei [[Schätzung]]en und die Originalreihe miteinander verglichen: |
|
| |
|
| {|
| | <iframe k="wiwi" p="examples/stat_Trend_Leistungsbilanzsalden_R00480004800000000000000_plot.html" /> |
| |<R output="display">
| |
| pdf(rpdf, width=10, height=7)
| |
| | |
| a = c(9478, 18003, -11031, -28480, -11741, 9866, 10573, 27940, 48327, 85793, 82097, 88336, 104057, 15309, -31916, -30221, -23357, -34191, -33818)
| |
| b = c(5483.3, -7169.3, -17084.0, -10118.3, 2899.3, 16126.3, 28946.7, 54020.0, 72072.3, 85408.7, 91496.7, 69234.0, 29150.0, -15609.3, -28498.0, -29256.3, -30455.3)
| |
| c = c(-4754.2, -4676.6, -6162.6, 1631.6, 16993.0, 36499.8, 50946.0, 66498.6, 81722.0, 75118.4, 51576.6, 29113.0, 6774.4, -20875.2, -30700.6)
| |
| d = c(-476.0, 2161.4, 6493.4, 20325.4, 36122.1, 50418.9, 63874.7, 64551.3, 56000.4, 44779.3, 29186.0, 12573.9, -4876.7)
| |
| | |
| t1 = ts(a, start=1977, end=1995)
| |
| t2 = ts(b, start=1978, end=1994)
| |
| t3 = ts(c, start=1979, end=1993)
| |
| t4 = ts(d, start=1980, end=1992)
| |
| options(scipen=5)
| |
| plot(t1, xlab="Period", ylab="Million DM", yaxt="n", lwd=2)
| |
| axis(2, at=c(0, 50000, 100000))
| |
| lines(t2, col="green", lwd=2)
| |
| lines(t3, col="red", lwd=2)
| |
| lines(t4, col="blue", lwd=2)
| |
| | |
| </R>
| |
| |}
| |
| | |
| Man erkennt zwei wichtige Eigenschaften des Verfahrens: | | Man erkennt zwei wichtige Eigenschaften des Verfahrens: |
|
| |
|
Grundbegriffe
Trend einer Zeitreihe
Die Zerlegung einer Zeitreihe beginnt mit der Extraktion der langfristigen Tendenz (Trend) aus den Beobachtungen.
Dazu stehen verschiedene Methoden, die jeweils zu unterschiedlichen Trendlinien für ein und diesselbe Reihe führen, zur Verfügung.
Die Auswahl einer dieser Methoden erfordert generell ein Abwägen zwischen Vor- und Nachteilen.
In diesem Abschnitt werden die Methode der gleitenden Durchschnitte und die Methode der kleinsten Quadrate vorgestellt.
Methode der gleitenden Durchschnitte
Filter
Der geschätzte Trend ist bei diesem Verfahren zu jedem Zeitpunkt ein gewichtetes Mittel aus den Originaldaten mehrerer Perioden:

mit

Die Gesamtheit der Gewichte  nennt man Filter.
nennt man Filter.
Die Wahl des Filters hängt von der Art saisonaler Schwankungen und der gewünschten Glättung ab. Meist werden symmetrische Filter, die (ausgehend von Periode  ) Vergangenheit und Zukunft gleichgewichten, verwendet.
) Vergangenheit und Zukunft gleichgewichten, verwendet.
Filter, deren Gewichte  für alle
für alle  gleich sind, bilden sogenannte einfache gleitende Durchschnitte, alle anderen führen zu gewichteten gleitenden Durchschnitten.
gleich sind, bilden sogenannte einfache gleitende Durchschnitte, alle anderen führen zu gewichteten gleitenden Durchschnitten.
Stützbereich
Der Bereich aus den Originaldaten, über den der gewichtete Durchschnitt gebildet wird, heisst Stützbereich.
Aus Prinzip kann die Reihe des geschätzten Trends höchstens so lang sein wie die Originalreihe (Gleichheit, wenn  ).
).
Je größer man den Stützbereich wählt, umso weniger Trendwerte können berechnet werden und umso glatter wird die resultierende Trendreihe.
Symmetrischer Filter
Symmetrische Filter ( ) werden meist so angegeben, dass die
) werden meist so angegeben, dass die  einzelnen Gewichte nebeneinander in eckigen Klammern stehen.
einzelnen Gewichte nebeneinander in eckigen Klammern stehen.
Die folgenden Filter finden bei der Glättung von saisonalen Zeitreihen Anwendung, weil sie für die Trendberechnung die
periodischen Schwankungen aus den Originaldaten "herausfiltern".
![{\displaystyle \left[{\frac {1}{4}},\;{\frac {1}{2}},\;{\frac {1}{4}}\right]\quad (a=1)}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=9c87ea2e814f4cd7760ccac8e5930471&mode=mathml)
![{\displaystyle \left[{\frac {1}{8}},\;{\frac {1}{4}},\;{\frac {1}{4}},\;{\frac {1}{4}},\;{\frac {1}{8}}\right]\quad (a=2)}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=e6d21a4346984e307ff02da8c13ddc7a&mode=mathml)
![{\displaystyle \left[{\frac {1}{8}},\;{\frac {1}{4}},\;{\frac {1}{4}},\;{\frac {1}{4}},\;{\frac {1}{8}}\right]\quad (a=2)}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=a4baea7ab196b66726d756807bbd02b7&mode=mathml)
![{\displaystyle \left[{\frac {1}{16}},\;{\frac {1}{8}},\;{\frac {1}{8}},\;{\frac {1}{8}},\;{\frac {1}{8}},\;{\frac {1}{8}},\;{\frac {1}{8}},\;{\frac {1}{8}},\;{\frac {1}{16}}\right]\quad (a=4)}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=c80b891f90bcbdce67a96624ce5a3444&mode=mathml)
![{\displaystyle \left[{\frac {1}{24}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{12}},\;{\frac {1}{24}}\right]\quad (a=6)}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=9c277da711f16aed2b9ea5c52072d267&mode=mathml)
Methode der kleinsten Quadrate
Eine zweite Möglichkeit den Trend einer Zeitreihe zu ermitteln, bietet die Methode der kleinsten Quadrate, wie sie im Kapitel "Schätzung der Regressionsparameter" vorgestellt wurde.
Man wählt eine Familie von Funktionen, durch die der Trend in Abhängigkeit von der Zeit  beschrieben werden soll und schätzt dann deren Parameter.
beschrieben werden soll und schätzt dann deren Parameter.
Diese Parameterschätzer minimieren die Summe der quadratischen Abweichungen des Trends von den Originaldaten:

Exemplarisch werden im folgenden die Schätzer für eine einfache lineare Trendfunktion und für einen Exponentialtrend hergeleitet.
Lineare Trendfunktion
Unterstellt sei eine lineare Abhängigkeit der Variablen  von der Zeit
von der Zeit  in der Form
in der Form

Die Summe der Residuenquadrate in Abhängigkeit von den Parametern  und
und  ist
ist

Die Minimierung ergibt die Parameterschätzer


Exponentialtrend
Unterstellt sei eine exponentielle Abhängigkeit der Variablen  von der Zeit
von der Zeit  in der Form
in der Form

bzw. in logarithmierter Form

Die Minimierung ergibt die Parameterschätzer


Zusatzinformationen
Informationen zur Ordnung des gleitenden Durchschnitts
Stützbereich: Anzahl  der Werte, die in die Mittelwertberechnung eingehen.
der Werte, die in die Mittelwertberechnung eingehen.
- Ungerade Ordnung


- Gerade Ordnung

![{\displaystyle X_{t}^{*}={\frac {1}{2k}}\cdot \left[{\frac {1}{2}}\cdot X_{t-k}+{\frac {1}{2}}\cdot X_{t+k}+\sum _{i=t-(k-1)}^{t+(k-1)}X_{i}\right]\qquad t=k+1,\ldots ,T-k}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=7e62005bc85d9985c18250c33d19e5a1&mode=mathml)
- Beispiel für ungerade Ordnung:

|

|

|

|

|

|

|
 --- ---
|
 --- ---
|

|

|
 --- ---
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
 --- ---
|

|
 --- ---
|
 --- ---
|
- Beispiel für gerade Ordnung:

|

|

|

|

|

|

|
 --- ---
|
 --- ---
|

|
![{\displaystyle \,x_{2}^{*}={\frac {1}{2}}\cdot \left[{\frac {1}{2}}\cdot x_{1}+{\frac {1}{2}}\cdot x_{3}+x_{2}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=4a138b1fc465ee5e352e3261773e6923&mode=mathml)
|
 --- ---
|

|
![{\displaystyle \,x_{3}^{*}={\frac {1}{2}}\cdot \left[{\frac {1}{2}}\cdot x_{2}+{\frac {1}{2}}\cdot x_{4}+x_{3}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=e21abb80f7911956561b3b4eff6d1194&mode=mathml)
|
![{\displaystyle \,x_{3}^{*}={\frac {1}{4}}\cdot \left[{\frac {1}{2}}\cdot x_{1}+{\frac {1}{2}}\cdot x_{5}+\sum _{i=2}^{4}x_{i}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=2c835abfc71b68515404baae43a89e49&mode=mathml)
|

|
![{\displaystyle \,x_{4}^{*}={\frac {1}{2}}\cdot \left[{\frac {1}{2}}\cdot x_{3}+{\frac {1}{2}}\cdot x_{5}+x_{4}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=d3c24f57302d68221022be2f25712885&mode=mathml)
|
![{\displaystyle \,x_{3}^{*}={\frac {1}{4}}\cdot \left[{\frac {1}{2}}\cdot x_{2}+{\frac {1}{2}}\cdot x_{6}+\sum _{i=3}^{5}x_{i}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=c70257f6f596c8c12086419821f7a144&mode=mathml)
|

|

|

|

|
![{\displaystyle \,x_{T-2}^{*}={\frac {1}{2}}\cdot \left[{\frac {1}{2}}\cdot x_{T-3}+{\frac {1}{2}}\cdot x_{T-1}+x_{T-2}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=b4dd52f43fe8e228a07f6e270f60d80c&mode=mathml)
|
![{\displaystyle \,x_{T-2}^{*}={\frac {1}{4}}\cdot \left[{\frac {1}{2}}\cdot x_{T-4}+{\frac {1}{2}}\cdot x_{T}+\sum _{i=T-3}^{T-1}x_{i}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=63151091d96a7ad927a6142cb8f0982d&mode=mathml)
|

|
![{\displaystyle \,x_{T-1}^{*}={\frac {1}{2}}\cdot \left[{\frac {1}{2}}\cdot x_{T-2}+{\frac {1}{2}}\cdot x_{T}+x_{T-1}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=a1888108704fba1dc0cecb367284de24&mode=mathml)
|
 --- ---
|

|
 --- ---
|
 --- ---
|
Beispiele
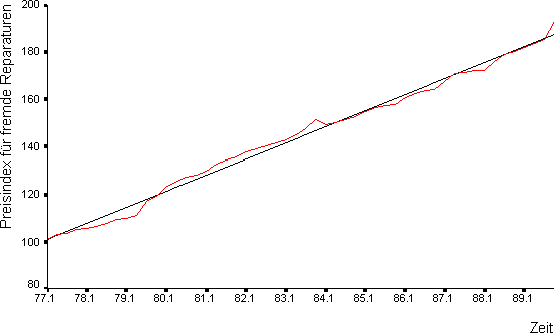
Preisindex (Lineare Trendfunktion)
Preisindex für fremde Reparaturen und sonstige Dienstleistungen
Berlin, 1. Quartal 1977 - 4. Quartal 1989

 entspricht dem 4. Quartal 1976.
entspricht dem 4. Quartal 1976.
Anzahl der Telefone (Exponentialtrend)
Anzahl der Telefone in den USA (in 1000) 1900-1970


 entspricht 1899.
entspricht 1899.

PKW (Symmetrischer Filter)
Zulassungszahl neuer PKW in Berlin 1. Quartal 1977 - 4. Quartal 1989 (Quartalsdaten)
Filter: ![{\displaystyle \left[{\frac {1}{8}},\;{\frac {1}{4}},\;{\frac {1}{4}},\;{\frac {1}{4}},\;{\frac {1}{8}}\right]}](/mmstat/w/index.php?title=Spezial:MathShowImage&hash=368442475a09e1f4cc3d39df318998f2&mode=mathml)
rot: Originalzeitreihe
schwarz: geglättete Reihe (Trend)
Leistungsbilanzsalden
Die folgende Zeitreihe beschreibt die Entwicklung der Leistungsbilanzsalden (in Mio Mark) der Bundesrepublik Deutschland in den Jahren 1977 - 1995:
Der Trend dieser Zeitreihe soll mit der Methode der gleitenden Durchschnitte geschätzt werden. Hierzu verwendet man die Formel

Da ausgehend von einem Zeitpunkt  Vergangenheits- und Zukunftswerte gleichgewichtet in die Trendschätzung eingehen sollen, wird
Vergangenheits- und Zukunftswerte gleichgewichtet in die Trendschätzung eingehen sollen, wird  gewählt.
gewählt.
Zur Glättung von Jahresdaten verwendet man einen einfachen gleitenden Durchschnitt, bei dem die Gewichte  für alle
für alle  identisch sind.
identisch sind.
Die Gewichte müssen sich über den gesamten Stützbereich zu 1 aufaddieren. Also gilt:
 für alle
für alle 
In der folgenden Tabelle wurde der gleitende Durchschnitt  jeweils für
jeweils für  und
und  berechnet.
berechnet.
| Jahr
|

|
Leistungsbilanz
|

|

|

|

|

|

|
| 1977
|
1
|
9478
|
|
|
|
| 1978
|
2
|
18003
|
5483,3
|
|
|
| 1979
|
3
|
-11031
|
-7169,3
|
-4754,2
|
|
| 1980
|
4
|
-28480
|
-17084,0
|
-4676,6
|
-476,0
|
| 1981
|
5
|
-11741
|
-10118,3
|
-6162,6
|
2161,4
|
| 1982
|
6
|
9866
|
2899,3
|
1631,6
|
6493,4
|
| 1983
|
7
|
10573
|
16126,3
|
16993,0
|
20325,4
|
| 1984
|
8
|
27940
|
28946,7
|
36499,8
|
36122,1
|
| 1985
|
9
|
48327
|
54020,0
|
50946,0
|
50418,9
|
| 1986
|
10
|
85793
|
72072,3
|
66498,6
|
63874,7
|
| 1987
|
11
|
82097
|
85408,7
|
81722,0
|
64551,3
|
| 1988
|
12
|
88336
|
91496,7
|
75118,4
|
56000,4
|
| 1989
|
13
|
104057
|
69234,0
|
51576,6
|
44779,3
|
| 1990
|
14
|
15309
|
29150,0
|
29113,0
|
29186,0
|
| 1991
|
15
|
-31916
|
-15609,3
|
6774,4
|
12573,9
|
| 1992
|
16
|
-30221
|
-28498,0
|
-20875,2
|
-4876,7
|
| 1993
|
17
|
-23357
|
-29256,3
|
-30700,6
|
|
| 1994
|
18
|
-34191
|
-30455,3
|
|
|
| 1995
|
19
|
-33818
|
|
|
|
Wenn  ist, kann man für die Periode
ist, kann man für die Periode  keinen Trend schätzen, weil der Wert der Zeitreihe in
keinen Trend schätzen, weil der Wert der Zeitreihe in  unbekannt ist.
unbekannt ist.
Für  ist der geschätzte Trend dann
ist der geschätzte Trend dann 
In der folgenden Grafik werden die drei Schätzungen und die Originalreihe miteinander verglichen:
Man erkennt zwei wichtige Eigenschaften des Verfahrens:
- Je größer der Stützbereich, über den der Trend geschätzt wurde (also je größer
 ), umso mehr Trendwerte konnten nicht geschätzt werden.
), umso mehr Trendwerte konnten nicht geschätzt werden.



