Graphische Darstellung eindimensionaler Verteilungen: Unterschied zwischen den Versionen
Aus MM*Stat
| Zeile 245: | Zeile 245: | ||
Die Untersuchungsergebnisse lassen sich auch in grafischer Form, beispielsweise anhand eines [[Säulendiagramm]]s oder [[Kreisdiagramm]]s darstellen. | Die Untersuchungsergebnisse lassen sich auch in grafischer Form, beispielsweise anhand eines [[Säulendiagramm]]s oder [[Kreisdiagramm]]s darstellen. | ||
<iframe k="wiwi" p="examples/ | <iframe k="wiwi" p="examples/stat_Eindimensional_Eindimensional_Beispiel_Berufe_R00480004801536915426039_plot.html" /> | ||
Aus den Grafiken lässt sich leicht der große Anteil erkennen, den die Arbeiter und Angestellten im Verhältnis zu den übrigen [[Merkmalsausprägung|Ausprägungen]] bilden. | Aus den Grafiken lässt sich leicht der große Anteil erkennen, den die Arbeiter und Angestellten im Verhältnis zu den übrigen [[Merkmalsausprägung|Ausprägungen]] bilden. | ||
Version vom 14. September 2018, 10:57 Uhr
Graphische Darstellung eindimensionaler Verteilungen
Höhenproportionale Darstellung
Eine Darstellung wird als höhenproportional bezeichnet, wenn allein die Höhe bzw. Länge des Balkens bzw. Stabes eine Aussage über die darzustellende Größe trifft.
Flächenproportionale Darstellung
Eine Darstellung wird als flächenproportional bezeichnet, wenn die darzustellenden Größen als Flächen abgebildet werden, wobei sich die Flächeninhalte proportional zu den darzustellenden Größen verhalten.
Grafische Darstellung diskreter Merkmale
Für die grafische Darstellung der eindimensionalen Häufigkeitsverteilung diskreter Merkmale gibt es verschiedene Möglichkeiten: Säulen- bzw. Balkendiagramm, Kreisdiagramm, Rechteck- bzw. Flächendiagramm, Stab- bzw. Liniendiagramm, Piktogramm oder Kartogramm.
Säulen- oder Balkendiagramm
Das Säulen- oder Balkendiagramm dient der grafischen Darstellung der empirischen Häufigkeitsverteilung vor allem von nominalskalierten und ordinalskalierten Merkmalen, aber auch von metrisch skalierten diskreten Merkmalen mit wenigen Merkmalsausprägungen.
Ein Balkendiagramm stellt die Häufigkeit jeder Merkmalsausprägung als separaten Balken dar. Dazu werden auf der Abszissenachse die Merkmalsausprägungen und auf der Ordinatenachse die beobachtete absolute oder relative Häufigkeit der jeweiligen Merkmalsausprägung abgetragen.
Im Allgemeinen handelt es sich hierbei um eine höhenproportionale Darstellung.
In der folgenden Grafik werden die relativen Häufigkeiten in Prozent verwendet:
Kreisdiagramm
Ein Kreisdiagramm stellt die Häufigkeit jeder Merkmalsausprägung durch die Aufteilung einer Kreisfläche in Sektoren dar.
Im Allgemeinen handelt es sich um eine flächenproportionale Darstellung.
Rechteck- oder Flächendiagramm
Ein Rechteck- oder Flächendiagramm stellt die Häufigkeit jeder Merkmalsausprägung durch die Aufteilung einer Fläche in einzelne Bereiche dar.
Im Allgemeinen handelt es sich um eine flächenproportionale Darstellung.
In der folgenden Grafik werden die relativen Häufigkeiten in Prozent verwendet:
Stab- oder Liniendiagramm
Ein Stab- oder Liniendiagramm stellt die Häufigkeit jeder Merkmalsausprägung durch die Höhe von Säulen dar (vgl. Säulendiagramm).
Im Allgemeinen handelt es sich um eine höhenproportionale Darstellung.
Piktogramm
Ein Piktogramm stellt die Häufigkeit jeder Merkmalsausprägung mit unterschiedlich großen Bildsymbolen oder einer verschieden großen Anzahl von Bildsymbolen dar. Dabei muss die ausgewählte Größe des Bildsymbols bzw. die Anzahl der Bildsymbole die dafür stehende Häufigkeit abbilden.
Kartogramm
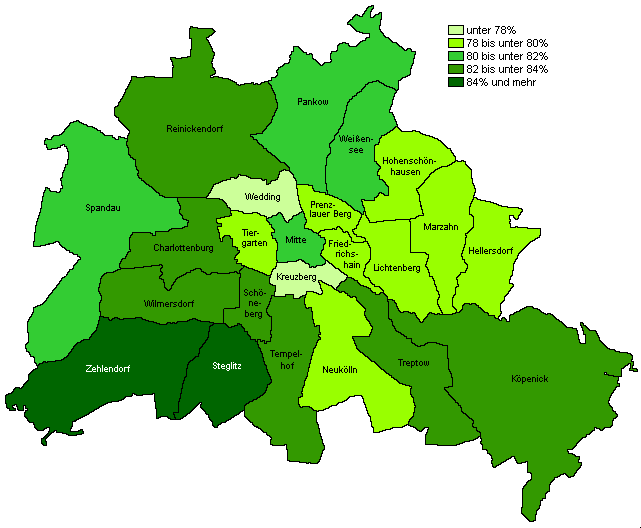
Ein Kartogramm stellt die Häufigkeit jeder Merkmalsausprägung innerhalb einer Landkarte dar.
Grafische Darstellung stetiger Merkmale
Histogramm
Die grafische Darstellung der Häufigkeiten eines stetigen klassierten Merkmals durch rechteckige Flächen wird als Histogramm bezeichnet. Es eignet sich auch zur Darstellung der Häufigkeiten diskreter Merkmale mit sehr vielen Merkmalsausprägungen, da solche Merkmale vielfach klassiert und als (quasi-)stetige Merkmale behandelt werden.
Die Klassengrenzen werden auf der Abszissenachse abgetragen. Über den Klassen werden Rechtecke in Höhe der Häufigkeitsdichten oder eingezeichnet.
Die Klassenhäufigkeit wird durch die Fläche des Rechtecks über der jeweiligen Klasse repräsentiert (flächenproportionale Darstellung). Die Verwendung der Häufigkeitsdichten ist unbedingt erforderlich, wenn ungleiche Klassenbreiten vorliegen.
Wird jedoch für alle Klassen eine gleiche Klassenbreite gewählt, kann auch eine höhenproportionale Darstellung verwendet werden, indem auf der Ordinatenachse die absoluten bzw. relativen Häufigkeiten abgetragen und die Rechtecke über den Klassen in Höhe der entsprechenden Häufigkeiten eingezeichnet werden.
Beispiel eines Histogramms für 2000 Beobachtungen des monatlichen persönlichen Nettoeinkommens (in Euro, Daten aus ALLBUS 2010):
{{#iframe:mmstat|mmstat_de/histogram_simple}}
Stengel-Blatt-Diagramm
Ein Stengel-Blatt-Diagramm (engl. stem-and-leaf-diagram) ist eine halbgrafische Darstellung der Werte einer Beobachtungsreihe eines metrisch skalierten Merkmals. Wie der Name vermuten lässt, besteht das Stengel-Blatt-Diagramm aus einem "Stamm" (stem) und "Blättern" (leaf).
Abhängig von der Anzahl der Beobachtungswerte gibt es zwei Grundvarianten des Stengel-Blatt-Diagramms.
Die erste Variante soll hier an einem kleinen Beispiel veranschaulicht werden. Die zweite Variante wird im Beispiel Netteinkommen weiter unten gezeigt.
Beobachtungsreihe: 32,32,35,36,40,44,47,48,53,57,57,100,105
Frequency Stem & Leaf
2,00 3 . 22
2,00 3 . 56
2,00 4 . 04
2,00 4 . 78
1,00 5 . 3
2,00 5 . 77
2,00 Extremes (>=100)
Stem width: 10,00
Each leaf: 1 case(s)
Unterhalb des Diagramms wird die Stamm-Einheit (stem width) angegeben. Das obige Diagramm hat z.B. eine "stem width" von 10, was bedeutet, dass der Stamm die Zehner-Ziffern enthält und die Blätter die Einer-Ziffern.
Der Stamm ist in diesem Beispiel auf zwei Zeilen aufgeteilt. Die erste Zeile, gekennzeichnet durch einen Stern (*), nimmt die Blätter von 0 bis 4, die zweite Zeile, gekennzeichnet durch einen Punkt (.), die Blätter von 5 bis 9 auf.
So hat beispielsweise der Beobachtungswert 47 den Stamm 4 und das Blatt 7. Jedes Blatt steht für einen Beobachtungswert ("Each leaf: 1 case"). Der Beobachtungswert 32 (Stamm 3, Blatt 2) kommt zweimal vor.
Weiterhin existieren zwei extrem große Beobachtungswerte (100 und 105), die als solche ausgewiesen sind.
Dotplot
Ein Dotplot ist eine zweidimensionale Darstellung eindimensionaler Daten, wobei auf der Abszissenachse der Bereich der beobachteten Merkmalswerte abgetragen wird.
Die einzelnen Beobachtungen werden über dieser Achse als Punkte (oder anderes Symbol) eingezeichnet.
Beispiel für 150 US-Stundenlöhne, wobei in dem oberen Teil der Grafik ein Dotplot für alle 150 Beobachtungen zusammen und im unteren Teil ein Dotplot mit der farbigen Trennung nach Männern und Frauen abgebildet ist.
Beispiele
Nettoeinkommen (Histogramm und Stengel-Blatt-Diagramm)
Histogramm
| statistische Einheit: | befragte, in Privathaushalten lebende deutsche Staatsangehörige im Alter von mindestens 18 Jahren |
| statistisches Merkmal: | monatliches persönliches Nettoeinkommen (€) |
| Anzahl der Beobachtungen : | 2000 |
Für die Erstellung jedes der nachfolgenden Histogramme wird von einer gleichen Klassenbreite der Einkommensklassen ausgegangen, so dass auf der Ordinatenachse die absoluten Häufigkeiten abgetragen wurden.
Zur Erstellung von Histogrammen, die entsprechende Details erkennen lassen, musste die Maßstabseinteilung der Ordinatenachse mit kleiner werdender Klassenbreite verändert werden. Beim Vergleich der Histogramme ist diese unterschiedliche Skalierung der Ordinatenachse zu beachten.
Die obenstehenden Grafiken verdeutlichen die Auswirkung unterschiedlicher Klassenbreiten auf das Erscheinungsbild. Durch das Variieren der Klassenbreiten soll erreicht werden, dass das Histogramm möglichst glatt (im Sinne eines gedachten Kurvenverlaufes durch die Höhe der Rechtecke über den Klassenmitten) wird, ohne jedoch die Besonderheiten der Daten aus den Augen zu verlieren.
Darstellung nach Geschlecht, bei einer Klassenbreite von 500 €:
Stengel-Blatt-Diagramm
Das Stengel-Blatt-Diagramm wird für alle 2000 Beobachtungen angegeben.
BEFR.: NETTOEINKOMMEN, OFFENE ABFRAGE Stem-and-Leaf Plot
Frequency Stem & Leaf
24,00 0 . 00111111
138,00 0 . 2222222222222333333333333333333333333333333333
194,00 0 . 44444444444444444444444444444444445555555555555555555555555555555
213,00 0 . 66666666666666666666666666666666666666777777777777777777777777777777777
211,00 0 . 8888888888888888888888888888888888899999999999999999999999999999999999
212,00 1 . 0000000000000000000000000000000000000000001111111111111111111111111111
200,00 1 . 2222222222222222222222222222222222222223333333333333333333333333333
181,00 1 . 4444444444444444444444444555555555555555555555555555555555555
132,00 1 . 66666666666666666666666666677777777777777777
88,00 1 . 88888888888888888899999999999
110,00 2 . 0000000000000000000000000000000011111
51,00 2 . 22222222222233333
56,00 2 . 4444555555555555555
23,00 2 . 6667777
20,00 2 . 8888899
46,00 3 . 0000000000000011
15,00 3 . 22223
86,00 Extremes (>=3400)
Stem width: 1000
Each leaf: 3 case(s)
Bei der obigen "großen" Version des Stengel-Blatt-Diagramms ist jeder Stamm auf fünf Zeilen aufgeteilt. Die erste Zeile nimmt die Blätter 0 und 1, die zweite Zeile die Blätter 2 und 3, die dritte Zeile die Blätter 4 und 5, die vierte Zeile die Blätter 6 und 7 und die fünfte Zeile die Blätter 8 und 9 auf.
Da die Stamm-Einheit (stem width) 1000 ist, sind die Blatt-Ziffern die Hunderter. Jedes Blatt beinhaltet 3 Fälle (Beobachtungen). Es gibt z.B. 8 befragte Personen mit einem Nettoeinkommen von 2400 bis unter 2500.
Insgesamt werden 86 extrem große Werte angezeigt, von denen einige aufgelistet werden.
"&" als Blatt beinhaltet eine restliche Anzahl von Beobachtungen - bei dem Stamm von 4 mit einem t sind z.B. 4 Fälle (befragte Personen) registriert.
Davon haben 2 Personen (da jedes Blatt 2 Fälle angibt) ein monatliches Nettoeinkommen von 4200 bis unter 4300 bei der Befragung angegeben.
Von den restlichen 2 Personen hat eine ein Nettoeinkommen von 4200 bis unter 4300 und die andere ein Nettoeinkommen 4300 bis unter 4400.
Es kann also weder ein Blatt mit der Ziffer 2 noch ein Blatt mit der Ziffer 3 angegeben werden, da jedes (in diesem Beispiel) zwei Fälle repräsentiert. Dies wird durch "&" gekennzeichnet.
Stellung im Beruf (Kreisdiagramm und Säulendiagramm)
Die erwerbstätigen Personen in der Bundesrepublik Deutschland (statistische Einheit) wurden im April 1991 hinsichtlich ihrer Stellung im Beruf (Merkmal ; nominalskaliert) untersucht.
| Stellung im Beruf | Erwerbstätige in 1000 | relative Häufigkeit |
|---|---|---|
| Arbeiter | 14.568 | 0,389 |
| Angestellte | 16.808 | 0,449 |
| Beamte | 2.511 | 0,067 |
| Selbständige | 3.037 | 0,081 |
| Mithelfende Familienangehörige | 522 | 0,014 |
| Summe | 37.466 | 1,000 |
Anhand der Tabelle lässt sich beispielsweise ersehen, dass 16.808.000 der untersuchten Personen in einem Angestelltenverhältnis arbeiten. Das entspricht einem Anteil von 44,9% an der Gesamtzahl aller Erwerbstätigen.
Die Untersuchungsergebnisse lassen sich auch in grafischer Form, beispielsweise anhand eines Säulendiagramms oder Kreisdiagramms darstellen.
Aus den Grafiken lässt sich leicht der große Anteil erkennen, den die Arbeiter und Angestellten im Verhältnis zu den übrigen Ausprägungen bilden.
Haushaltsgröße (Säulendiagramm)
Zur Untersuchung der Entwicklung der Haushaltsgrößen in den alten Bundesländern wurden diese zu verschiedenen Zeitpunkten des 20. Jahrhunderts statistisch erfasst.
| statistische Einheit: | Haushalte |
| statistisches Merkmal: | Haushaltsgröße |
| kardinalskaliert, diskret | |
| Häufigkeiten: | prozentual, relativ |
Die folgende Häufigkeitstabelle ermöglicht einen zahlenmäßigen Vergleich über die verschiedenen Zeitpunkte auf Grundlage der relativen Häufigkeiten.
| Haushaltsgröße | 1900 | 1925 | 1950 | 1990 |
|---|---|---|---|---|
| 1 | 7,1 | 6,7 | 19,4 | 35,0 |
| 2 | 14,7 | 17,7 | 25,3 | 30,2 |
| 3 | 17,0 | 22,5 | 23,0 | 16,7 |
| 4 | 16,8 | 19,7 | 16,2 | 12,8 |
| 5 und mehr | 44,4 | 33,3 | 16,1 | 5,3 |
| Summe | 100,0 | 100,0 | 100,0 | 100,0 |
Erleichtert wird dieser Vergleich durch die grafische Darstellung der relativen Häufigkeiten zu den verschiedenen Zeitpunkten in Säulendiagrammen.
Die Diagramme verdeutlichen sehr anschaulich die Verschiebung der Haushaltsgröße vom Vielpersonenhaushalt zum Haushalt mit nur wenigen Mitgliedern im letzten Jahrhundert.
Benzinverbrauch (Histogramm)
Von 74 verschiedenen Autotypen wurde der Benzinverbrauch in "miles per gallon" (mpg) gemessen - Umrechnung in l/100km:
Das Ergebnis der Untersuchung lässt sich übersichtlich in Form einer Häufigkeitstabelle darstellen:
| Benzinverbrauch (MPG)
|
absolute Häufigkeit
|
relative Häufigkeit
|
| von 12 bis unter 15 | 8 | 0,108 |
| von 15 bis unter 18 | 10 | 0,135 |
| von 18 bis unter 21 | 20 | 0,270 |
| von 21 bis unter 24 | 13 | 0,176 |
| von 24 bis unter 27 | 12 | 0,162 |
| von 27 bis unter 30 | 4 | 0,054 |
| von 30 bis unter 33 | 3 | 0,041 |
| von 33 bis unter 36 | 3 | 0,041 |
| von 36 bis unter 39 | 0 | 0,000 |
| von 39 bis unter 42 | 1 | 0,013 |
| Summe | 74 | 1.000 |
Die Häufigkeitsverteilung lässt sich in Form eines Histogramms mit der gleichen Klassenbreite wie in der Häufigkeitstabelle (3 Meilen) grafisch veranschaulichen. Auf der Ordinatenachse werden die Häufigkeitsdichten abgetragen.
Sowohl aus der Häufigkeitstabelle als auch aus dem Histogramm lässt sich erkennen, dass der größte Teil der untersuchten Autotypen mit einer Gallone 18 bis 21 Meilen zurücklegt.
Kriminalitätsraten (Interaktives Histogramm)
Für verschiedene Variablen (u.a. Verbrechen pro 1000 Einwohner in 1986) pro Bundesstaat können Sie die Anzahl der Klassen variieren.